Review topics for final exam
2.1 – one variable linear equations
solve equations (isolate x)
including those with fractions or decimals
2.5 – one variable linear inequalities
solve inequalities (isolate x; remember when to flip the symbol)
including those with fractions or decimals
2.6 – set operations - union, intersection
find intersection ( ∩ or “and”) of two sets
find union (∪ or “or”) of two sets
solve compound inequalities (with “and” or “or”)
3.1 - rectangular coordinate system (x-y plane)
quadrants
plot ordered pairs
graph any equation by using an x-y table
find x- and y- intercepts (from a graph or from an equation)
midpoint*
3.2 and 3.3 – graphs of linear equations
find slope from 2 points (given the graph or just ordered pairs)
don’t forget slopes for horizontal and vertical
graph lines
given the slope and any point on the line
given an equation
use different forms of linear equations - slope-intercept, point-slope
what important values are in these?
how/when do you use each?
horizontal lines (y = some #)
vertical lines (x = some #)
find equations of parallel & perpendicular lines and their slopes
given a graph, use one of the linear forms to write an equation of the line
remember for word problems: y = mx+b
m = rate of change (increase)
b = initial/starting value
3.4 – 2 variable linear inequalities
graph these inequalities
dashed or solid line?
shade up or down? left or right?
graph compound inequalities
same thing, but what part gets shaded by BOTH inequalities?
3.5 – relations and functions
different forms of relations
mapping diagram
set of ordered pairs
equation
graph
find domain and range of relations (from looking at any of the above forms)
from a graph: look left to right for domain; look bottom to top for range
definition of a function
decide if a relation is a function
if you see a graph -> use vertical line test
given a function, find the value of the function at a particular input
graph linear functions (just like linear equations, remember y = f(x)
5.5 Divide Polynomials
Divide by one term (monomial): divide each term on top one at a time (try to
cancel factors)
Divide by more than one term (polynomial):
Like long division
Remember what to do if you’re “missing” a term
6.1 – 6.3 Factoring Expressions
Take out a common factor from each term
Trinomials
Difference of squares (NOT sum):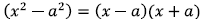
Difference of cubes: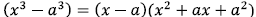
Sum of cubes :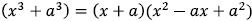
6.5 Solving Equations by Factoring (shows up at the end
of other problems too)
As soon as you seex2 and x :
Move every term to one side of the equation
Factor (using techniques from 6.1 – 6.3, depending on the problem)
Set each factor = 0, then solve each equation
7.1 Rational (fractional) Expressions
Find domain (remember denominator ≠0; set notation)
Write in lowest terms (factor, then try to cancel)
Multiply (straight across)
Divide (leave the first fraction alone, but multiply by the reciprocal of the
second fraction)
7.2 Adding and Subtracting Rational Expressions (just like adding/subt. any
fractions)
Need common denominator
Remember how to find LCD, then rewrite each fraction using that LCD
Add or subtract the numerators, keep the same denominator
7.3 Complex Fractions (fractions inside of fractions)
Remember what negative exponents mean (example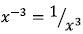
: )
Simplify using one of two methods (I think the second is easier)
Method 1: simplify the numerator, simplify the denom.,
then multiply the numerator by the reciprocal of the denominator
Method 2: multiply by
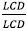(you want to get rid of all of the little fractions), then
simplify
7.4 Solving Rational Equations
1. Check the domain of x to know what solutions you have to eliminate
2. multiply both sides of equation by LCD (you want to get rid of fractions)
3. simplify, and solve for x
4. if any one of your solutions is not in the domain of x (check 1st step), then
throw it out
7.5 Applications
Take a formula, and solve for one of the variables
Use proportions
Problems with distance, rate, and time
5.1 Integer Exponents
Product Rule
Quotient Rule
Power Rules (3 different ones)
Negative exponents
a0=1(for any a)
Scientific Notation
8.1 Radical Expressions
Find roots
Graph radical functions (set up x-y table, plug in x’s, then use calculator to
help find y’s)
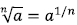may help to find a root using your calculator (or for different problems in 8.2)
8.2 Rational Exponents
Remember the rule: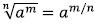 
to START simplifying expressions
Use it to write exponentials as radicals
Use it also to write radicals as exponentials
8.3 Simplifying Radicals
Product Rule
Quotient Rule
Rules for simplifying radicals (IMPORTANT):
1. no fractions in radicand
2. no radicals inside a denominator
3. the index and any exponents in the radicand must have no common factor
greater than 1
4. the radicand must have no factor raised to a power ≥ the index
8.4 Add/subtract radicals
Simplify each radical FIRST, then treat any common radicals like a variable
when you add/subt.
When fractions are involved, try to simplify each fraction FIRST, then add/subt.
using the LCD
8.5 Multiply/”Divide” Radicals
FOIL binomials
To “divide” - rationalize the denominator
When the denominator is a binomial, multiply the numerator and denom. by the
conjugate.
8.6 Solving EQUATIONS with Radicals
Step 1: Isolate one radical
Step 2: Use the power rule
Step 3: Solve the new equation
Step 4: Check EVERY possible solution in ORIGINAL equation
8.7 Complex Numbers
Use i to multiply, divide, and simplify radical expressions
Add/subtract complex numbers (combine like terms)
Multiply complex numbers (FOIL)
“Divide” complex numbers (use complex conjugate to get i out of the denominator)
9.1 and 9.2 Solving Quadratic Equations (if you can’t/don’t want to factor)
Sq. root property: As soon as you see x2 an term or
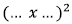(but NO plain terms):
Isolate the squared part
Take the square root of both sides (remember ±)
If you’re not done already, solve for x
As soon as you see an x2 term AND an x term:
Move every term to one side of the equation (need: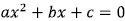
)
If you can’t/don’t want to factor – complete the square OR use quadratic formula
To complete the square:
1. If a≠1, divide every term by .
2. Move constant to the other side.
3. Take ½ of the number in front of x (remember you’ll use this answer later),
then square it.
4. Add that squared answer to both sides.
5. Factor the trinomial, but remember it should turn into
(x
then that ½ answer from before.)2
6. Use sq. root property, and solve.
Memorize the quadratic formula:
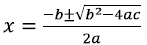
Don’t forget, if you have a neg. INSIDE of a sq. root,
that means you take it out and put on the OUTSIDE of the sq. root.
9.4 Applications of quadratic equations
Solve formulas for a different variable (using the techniques above).
Solve word problems (using the techniques above; you may also need to use
).
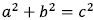9.5 and 9.6 Graphs of Quadratic Equations (Parabolas)
Remember how to graph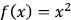 
(or really what it is/where it is on the coordinate
plane).
Use that graph to shift up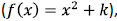
shift down
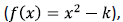shift left
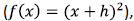shift right
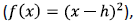or a combination of shifts.
Look at the a in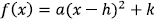 
or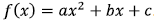
…
a>0 parabola opens up a<0: parabola opens down
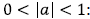parabola is wider than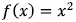
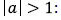parabola is narrower than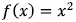
For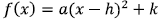
…
Vertex : (h, k) y-intercept: plug in 0 for x, and solve
For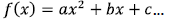
Vertex: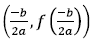 
or 
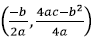y-intercept:(0,
c)
Remember how to find domain and range from a graph
(domain of a parabola is always(−∞, ∞) , but you’ll have to think about range more).
4.1 Systems of Linear Equations
To check if a solution (x, y) is correct, plug into BOTH original equations
Solve any system by using substitution, elimination, or graphing
Know how to recognize when there is NO solution or when there is an infinite #
of solutions
4.3 Applications of Systems of Equations
Step 1: read
Step 2: define variables for what you don’t know (usually what you’re asked to
find)
Step 3: write equations
Step 4: solve with substitution or elimination
Step 5: check answers
Problems with cost:
Try to add up to a total # of items bought/sold
AND/OR
Try to add up to a total amount of $ made/spent
Problems with a mixture:
Try to add up to the total amount mixed/split up
AND/OR
Try to add up to the total concentration/interest/cost
| Prev | Next |