Seventh Grade Math Test

18. On a Friday drive from St. Louis to Chicago, Aaron shares the driving with a friend. Before lunch, Aaron drove 1/3 of the 180 miles covered. After lunch, Aaron drove 1/4 of the 120 miles they had left. What fraction of the day 's trip did Aaron drive?

A. 3/10
B. 2/7
C. 7/12
D. 1/2
E. 2/5

19. Rutherford B. Hayes was elected President of the United States in a leap year in the 19th Century. The sum of the digits in that year is 22. What is the tens'; digit of that year?

A. 5
B. 6
C. 7
D. 8
E. 9

20. England and the United States have always agreed that “one million = 1,000,000”.
Until recently, the English defined a billion to be a million million.
What is the ratio between the former English billion and the current US billion?

A. 1
B. 10
C. 100
D. 1000
E. 1,000,000

21. On this regular octagon, a snail starts at A and crawls clockwise along the
edges. Where is the snail when the it has completed 2/3 of the distance
around the octagon?

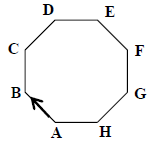
A. Between E and F
B. Point F
C. Between F and G
D. Point G
E. None of these

22. A 2 m deep 20 m by 12 m rectangular pool is filled with water. When all of this water is transferred into a 16 m by 16 m pool, how deep is the water?

A. 1.6 m
B. 1.75 m
C. 1.875 m
D. 2 m
E. 2.25 m

23. If today is Saturday, what day of the week will it be 2^7 days from now?

A. Saturday
B. Sunday
C. Monday
D. Tuesday
E. Wednesday

24. In basketball, a player can score via 3-point shots, 2-point field goals, or 1-point free throws. If Tonya makes seven 2-point field goals while scoring 34 points, what is the minimum number of free throws that she has made?

A. 0
B. 1
C. 2
D. 3
E. 4

25. On a day in June, sunrise is 6:00 am and sunset is 9:00 pm. At what time of that day is the number of hours past sunrise equal to twice the number of hours before sunset?

A. 11:00 am
B. 12:00 noon
C. 1:30 pm
D. 2:30 pm
E. 4:00 pm

26. Cheryl ran a 10 kilometer race in exactly 51 minutes. To the nearest tenth, what was her average speed in miles per hour? (Use: 1 mile = 1.61 km)

A. 7.3 mph
B. 7.6 mph
C. 8.1 mph
D. 8.4 mph
E. 19.0 mph

27. Two standard 6-sided dice are rolled. What is the probability that the sum is 10, 11, or 12?

A. 1/6
B. 3/11
C. 1/4
D. 1/12
E. 3/8

28. 8,000,000 is the product of two whole numbers, neither whole number contains the digit “0”. What is the positive difference between the two whole numbers?

A. 15,113
B. 25,550
C. 94,200
D. 106,117
E. 999,992

29. 37 divided by N leaves a remainder of 7. For how many different whole numbers N is this true?

A. 0
B. 1
C. 2
D. 3
E. 6

30. Emily, Sarah, and Andrea share a bowl of strawberries. First, Emily ate 1/3 of them. Then Sarah ate 1/3 of the remaining strawberries. Andrea ate the last 8 strawberries.
How many strawberries did Emily eat?

A. 6
B. 8
C. 12
D. 24
E. 48

31. Martha purchases 240 feet of fence for enclosing her rectangular garden. Her plan called for the width to be 40 feet. However, her neighbor Mrs. Euler convinced her to make the width 60 feet. Using the same 240 feet of fence, how many square feet larger is the rectangular garden Mrs. Euler suggested compared to the one Martha had planned?

32. Select any twenty consecutive three- digit whole numbers. Divide each of them by 20 and record each remainder. What is the sum of the twenty remainders?

A. 180
B. 190
C. 200
D. 205
E. 210

33. For the team she coaches, Brenda buys sodas at $0.75 each and hamburgers at $1.20 each. If she buys more hamburgers than sodas, buys at least one soda , and spends a total of $21.60 on sodas and hamburgers, what is the total number of hamburgers and sodas she buys?

A. 21
B. 22
C. 23
D. 24
E. 25

34. A 15-foot by 32-foot rectangular pool is surrounded by a 3-foot wide
walkway so that the pool and walkway make a larger rectangle.
How many 6-inch by 6-inch square tiles are required to pave this walkway?

A. 318
B. 636
C. 954
D. 1024
E. 1272

35. B and C are distinct digits in the 6-digit number N: N = 1B3,45C .
If N is divisible by 15, how many different numbers could N be?

A. 3
B. 4
C. 5
D. 6
E. 7

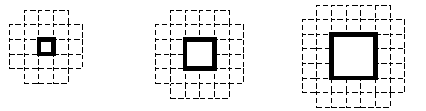
36. Unit squares (shown below) are used to build each pattern. The first three patterns are shown.
Not including the square hole , how many unit squares are needed to build the 20th pattern in this
sequence?

A. 140
B. 144
C. 164
D. 172
E. 176

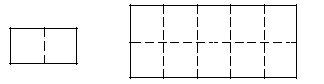
37. In how many distinct ways can five 1 by 2 tiles be used to cover a 2 by 5 rectangle?

A. 5
B. 6
C. 8
D. 9
E. 13

38. Fill each of the twelve blank cells with one digit, 0 through 9.
The letters A, B, C, and D each represent a 2-digit or 3-digit number from the corresponding row.
For example, A is the horizontal 3-digit number beginning in cell AE and B is the 2-digit
horizontal number beginning in cell BG. Similarly, E, F, G, and H each represent a 2-digit or
3-digit number from the corresponding column.
None of these eight 2-digit or 3-digit numbers begins with the digit “0”.

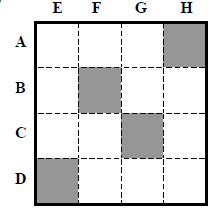
CLUES:
E = 5F D = 8H
E = A + 91 A = 4B

What is the sum of all twelve digits that you use?

A. 48
B. 49
C. 50
D. 51
E. 52

39. Gene and Anne have one coin and continue to flip it until one of them wins this game.
Gene wins if the sequence “Head-Head” appears before the sequence “Tail-Head”.
Anne wins if the sequence “Tail-Head” appears before the sequence “Head-Head”.
What is Anne’s probability of winning this game?

A. 1/4
B. 1/3
C. 1/2
D. 2/3
E. 3/4

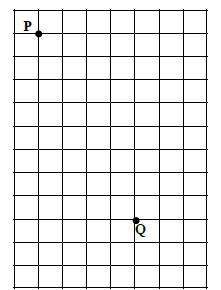
40.
On this grid of streets, each block is square and bicyclists
must stay on the streets. Therefore, the distance (the
length of a shortest path) between points P and Q is 8+4 =
12 blocks, not the length of the segment PQ =

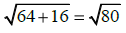blocks.

Pauline at P and Quincy at Q agree to meet at any
intersection T such that the shortest distance from P to T is
6 blocks and the shortest distance from Q to T is also 6
blocks. How many different intersections are possible
meeting points?

A. 0
B. 2
C. 4
D. 5
E. More than 5