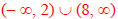Solving Inequalities Algebraically and Graphically
Objective:
In this lesson you learned how to solve linear inequalities,
inequalities involving absolute values, polynomial
inequalities, and rational inequalities .
Important Vocabulary Define each term or concept.
Solutions of an inequality All values of the variable for which the inequality is true.
Graph of an inequality The set of all points on the
real number line that represent
the solution set of an inequality.
Linear inequality An inequality in one variable (usually x) that can be
written in the
form ax + b < 0 or ax + b > 0,where a and b are real numbers with a ≠ 0.
Double inequality An inequality that represents two inequalities .
Critical numbers The x-values that make the polynomial
in a polynomial inequality
equal to zero.
Test intervals Open intervals along the real number line in which the
polynomial has
no sign changes .
| I. Properties of Inequalities
(Pages 54-55)
|
What you should learn How to recognize properties of inequalities |
| Solving an inequality in the variable
x means . . . finding all the values of x for which the inequality is true.
Numbers that are solutions of an inequality are said
to To solve a linear inequality in one variable, use
the properties When both sides of an inequality are multiplied or
divided by a Two inequalities that have the same solution set
are Complete the list of Properties of Inequalities
given below. |
|
| II. Solving a Linear Inequality (Pages 55-56) |
What you should learn How to use properties of inequalities to solve linear inequalities |
| Describe the steps that would be
necessary to solve the linear inequality 7x - 2 < 9x + 8 . Add 2 to
each side. Subtract 9x from each side, and combine like To use a graphing utility to solve the linear
inequality
The two inequalities - 10 < 3x and 14 ≥ 3x can be rewritten as |
|
| III. Inequalities Involving Absolute
Value (Page 57) |
What you should learn How to solve inequalities involving absolute values |
| Let x be a variable or an algebraic expression and let a be a real number such that a ≥ 0. The solutions of |x| < a are all values of x that lie between - a and a . The solutions of |x| > a are all values of x that are less than - a or greater than a . Example 1: Solve the
inequality: The symbol Example 2:
Write the following solution set using interval |
|
| IV. Polynomial Inequalities (Pages
58-60) |
What you should learn How to solve polynomial inequalities |
| Where can polynomials change signs ? Only at its zeros, the x-values that make the polynomial equal to zero. Between two consecutive zeros, a
polynomial must be . . . When the real zeros of a polynomial are put in order, they divide These zeros are the critical numbers of the inequality, Complete the following steps for determining the intervals on 1) Find all real zeros of the polynomial, and arrange the To approximate the solution of the polynomial inequality If a polynomial inequality is not given in general form, you |
|
Example 3: Solve x2 + x - 20 ≥ 0 .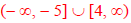 Example 4: Use a graph to solve the polynomial inequality |
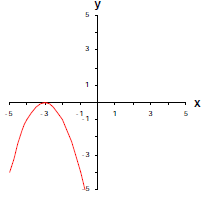 |
| V. Rational Inequalities (Page 61) | What you should learn How to solve rational inequalities |
| To extend the concepts of critical
numbers and test intervals to rational inequalities, use the fact that the value of a rational expression can change sign only at its zeros and its undefined values . These two types of numbers make up the critical numbers of a rational inequality. To solve a rational inequality, . . . first write the rational inequality in standard form. Then find the zeros and undefined values of the resulting rational expression. Form the appropriate test intervals and test a point from each interval in the inequality. Select the test intervals that satisfy the inequality as the solution set. Example 5: 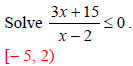 |
|
| Homework Assignment Page(s) Exercises |
|
| Prev | Next |
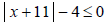
 is called a
union symbol and is used to
is called a
union symbol and is used to