Systems of Linear Equations
In Section 1.1 we gave a quadratic formula 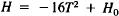 to model
to model
mathematically the height of an object dropped from a building
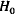 feet tall.
feet tall.
From this formula we could determine how long it took for an object to hit
the ground (see Example I of Section 1.1). The model involved a single
nonlinear equation with one variable to be determined . Nonlinear equations
in one variable are not difficult to derive and solve.
When many variables need to be determined, then almost surely the
mathematical model will be a system of linear equations . There are four
basic reasons for using linear models.
1. There is a rich theory for analyzing and solving systems of linear equations.
There is limited theory and no general solution techniques
for systems of nonlinear equations.
2. Systems of nonlinear equations involving several variables exhibit very
coml1lex behavior and we rarely understand real -world phenomena well
enough to use such complex models.
3. Small changes in coefficients in nonlinear systems can cause huge
changes in the behavior of the systems, yet precise values for these
coefficients are rarely known.
4. All nonlinear phenomena are approximately linear over small intervals;
that is, a complicated curve can be approximated by a collection of many
short line segments (see Figure 1.5).
Exercises 1-3 refer to the refinery model in Example 1.
1. Suppose that refinery 1 processes 15 barrels of petroleum, refinery 2
processes 20 barrels, and refinery 3 processes 60 barrels. With this
production schedule , for which product does production deviate the
most from the set of demands 500, 850, 1000?
2. Suppose that the demand for heating oil grows to 800 gallons, while
other demands stay the same. Find production levels of the three refineries
to meet approximately this new set of demands (by "approximately"
we mean with no product off by more than 30 gallons).
3. Suppose that refinery 3 is improved so that each barrel of petroleum
yields 8 gallons of heating oil, 10 gallons of diesel oil, and 20 gallons
of gasoline. Find production levels of the three refineries to meet
approximately
the demands (by "approximately" we mean with no product
off by more than 30 gallons).
4. Consider the following refinery model. There are three refineries 1, 2, and 3
and from each barrel of crude petroleum, the different refineries
produce the following amounts (measured in gallons) of heating oil,
diesel oil, and gasoline.
|
|
Refinery 1 | Refinery 2 | Refinery 3 |
| Heating oil | 6 | 3 | 2 |
| Diesel oil | 4 | 6 | 3 |
| Gasoline | 3 | 2 | 6 |
Suppose that we have the following demand:
280 gallons of heating oil,
350 gallons of diesel oil, and
350 gallons of gasoline.
(a) Write a system of equations whose solution would determine production
levels to yield the desired amounts of heating oil, diese
oil, and gasoline. As in Example 1, let xi be the number of barrel
processed by the ith refinery.
(b)
Find an approximate solution to this system of equations with no
product off by more than 30 gallons from its demand.
5. Repeat the refinery model in Exercise 4 with new demand levels of 500
gallons heating oil, 300 gallons diesel oil, and 600 gallons gasoline
Try to find an approximate solution (within 30 gallons) with this set of
demands. Something is going wrong and there is no valid set of production
levels to attain this set of demands. What is invalid about the
solution to this refinery problem?
Extra Credit: Try to explain in words why this set of demands is
unattained while the demands in Exercise 4 were attainable.
6. The staff dietician at the California Institute of Trigonometry has to
make up a meal with 600 calories, 20 grams of protein, and 200 milligrams
of vitamin C. There are three food types to choose from: rubbery
jello, dried fish sticks, and mystery meat. They have the following
nutritional content per ounce.
|
|
Jello | Fish Sticks | Mystery Meat |
| Calories | 10 | 50 | 200 |
| Protein | 1 | 3 | .2 |
| Vitamin C | 30 | 10 | o |
(a) Make a mathematical model of the dietician's problem
with a system
of three linear equations.
(b) Find an approximate solution (accurate to within 10%).
7. A furniture manufacturer makes tables, chairs, and sofas. In one month,
the company has available 300 units of wood, 350 units of labor, and
225 units of upholstery. The manufacturer wants a production schedule
for the month that uses all of these resources. The different products
require
the following amounts of the resources.
| Table | Chair | Sofa | |
| Wood | 4 | 1 | 3 |
| Labor | 3 | 2 | 5 |
| Upholstery | 2 | 0 | 4 |
(a) Make a mathematical model of this production problem.
(b) Find an approximate solution (accurate to within 10%).
8. A company has a budget of $280,000 for computing equipment. Three
types of equipment are available: microcomputers at $2000 a piece,
terminals at $500 a piece, and word processors at $5000 a piece. There
should be five times as many terminals as microcomputers and two
times as many microcomputers as word processors. Set this problem up
as a system of three linear equations. Determine approximately how
many machines of each type there should be by solving by trial-and-error.
Note: Check your answer by expressing the numbers of
terminals and
microcomputers in terms of the number of word processors and solving
the remaining single equation in one unknown.
Exercises 9-11 are based on the Leontief model in Example 2.
9. If we produced 300 units of energy, 250 units of construction, 160 units
of transportation, and 40 units of steel, what would be the largest deviation
between supply and demand among the four commodities?
10. Start the iteration procedure followed in (9), (10), and (II) with an
initial set of supplies equal to the consumer demands, that is,
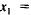
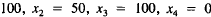 . Compute the right sides of
the
. Compute the right sides of
the
equations in (6) with this set of x1's and let the resulting numbers be
the
new values for 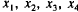 ; compute the right sides
again with
; compute the right sides
again with
these new xis; and so on. Do this iteration five times. Do the successive
sets
of xis appear to be converging toward the equilibrium values given
at the end of
Example 2?
11.
This exercise explores the effect on all industries of changes in one
industry.
Quadrupling the price of petroleum had a widespread effect
on all industrial
sectors in the 1970s. But smaller changes in one seemingly
unimportant industry
can also result in important changes in many
other industries.
(a)
Change the system of equations in the Leontief model in (6) by
decreasing the
coefficient of x1(energy) in the construction equation
from .3 to .2 (this is
the result of new energy efficiencies in construction
equipment). We want to
know how this change affects
our economy. Iterate five times, as in Exercise 10,
with this altered
system using as starting xi's the equilibrium values for the
original
model: 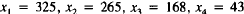 .
.
(b) Repeat part (a), but now decrease the coefficient of x4 (steel) in the
transportation equation from .2 to .1.
(c) Repeat part (a), but now increase the coefficient of x2 (construction)
in the
energy equation from .2 to .3.
12. Consider the Leontief system
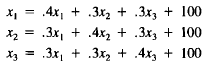
Here the column sums are1, violating the Leontief input
constraint
given in the text. Show that this system cannot have a solution.
Hint: Add the three equations together.
Extra Credit: Try to explain in economic terms why no solution exists.
13. (a)
Rewrite the refinery model's equations in (3) to look like Leontief
equations as follows. Divide the first equation by 20 (the coefficient
of x1 in that equation), divide the second equation by 14, and divide
the third equation by 12. Next move the x2 and x3 terms in the new
first equation over to the right side, leaving just x1 on the left (the
new equation should be 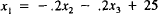 ; similarly, in
; similarly, in
the second equation leave just x2 on the left and in the third equation
leave just x3
on the left. Note that the Leontief input constraint
about column sums is not satisfied by this system.
(b) Use the iteration method introduced in equations (9), (10), and (11)
(see also Exercise 10) to get an approximate solution to the refinery
problem (do five iterations, starting with the "consumer demands"
of 25, 50, 100).
14. (a) Rewrite the refinery model's equations in (3) to look somewhat like
Leontief equations as follows. In the first equation, move the x2
and
x3 terms
to the right side and also move 19 of the 20 units of the
x1 term to the right,
leaving just x1 on the left (the equation is
now 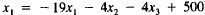 ).
Similarly, in the second
).
Similarly, in the second
equation leave just x2 on the left; move everything
else to the right
side. In the third equation leave just x3 on the left. Note
that Leontief's
input constraint about column sums is far from satisfied by this
system.
(b) Try using the iteration method introduced in equations (9), (10),
and (II)
(see also Exercise 10) to get an approximate solution to
the refinery problem
(do five iterations starting with the guess of
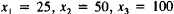 ).
Does the iteration process seem to
).
Does the iteration process seem to
be converging?
| Prev | Next |