Working with Circles
Definition of a circle: A circle is the set of all
points that are the same distance from a fixed
point called the center. The distance from the center to any point on the circle
is called the
radius.
Topics covered in this handout:
1. Standard form of the equation of a circle
2. Completing the square for variables in the equation of a circle
3. Finding the center and radius of a circle
4. Graphing a circle
Standard Form of a Circle:
The standard form of the equation of a circle with center (h, k) and radius r is
(x – h)^2 + (y – k)^2 = r^2
Notice the negative signs in front of the h and the k. You must take this into
account when
writing the equation of a circle.
Example: Let (h, k) = (4, -7) and r = 3. Write the
equation of this circle in standard form.
Plugging into the equation 4 for h, -7 for k, and 3 for r you get
(x – (4))^2 + (y – (-7))^2 = 3^2
(x – 4)^2 + (y + 7)^2 = 9
Completing the Square:
The equation of a circle is not always given to you in standard form. So, you
have to use the
method of completing the square to rewrite the equation into standard form.
First, let’s look at completing the square for any type of equation that has one
variable.
Example: x^2 + 8x + 14 = 0
First, subtract 14 from both sides to get only terms with an x or x^2 on one
side.
x^2 + 8x = -14
You need to find a number that you can add to the left-hand side of the equation
so it will factor
as a perfect square .
x^2 + 8x + __ = -14
To find this, divide the number in front of the x by 2
(i.e. 8/2 = 4). Then, square the result you
just obtained (i.e. (4)^2 = 16). Add this number to the left-hand side of the
equation. You must
also add this number to the right -hand side of the equation so that you don’t
change the original
equation ( Remember in algebra , if you do it to one side of the equation, you
must do it to the
other side).
x^2 + 8x + 16 = -14 + 16
(x + 4)(x + 4) = 2
(x + 4)^2 = 2
[Hint: You computed 8/2 = 4 above, and the perfect square
ended up being
(x + 4)^2. This will always happen when completing the square.]
Example: Let’s now complete the square for both variables in the equation of a circle.
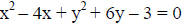 |
|
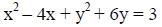 |
[ Terms with a variable on one side , constants on the other side] |
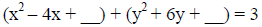 |
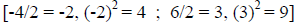 |
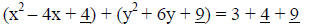 |
|
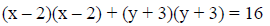 |
|
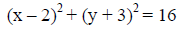 |
[Remember the hint from above -4/2 = -2 and 6/2 = 3] |
Finding the Center and Radius of a Circle:
Find the center and radius of a circle that is written in standard form.
Example: (x – 5)^2 + (y + 6)^2 = 49
[Remember, the standard form of the equation of a circle is (x-h)^2 + (y-k)^2 =
r^2 where (h, k) is the
center and r is the radius.]
Center: (h, k) = (5, -6)
Radius: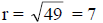
Example:
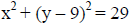
[Think of it as 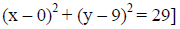
Center: (0, 9)
Radius: 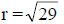
Example: Find the center and radius of equation that is not given in standard form.
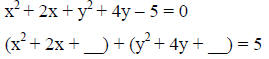 |
|
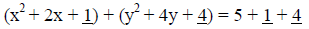 |
[Complete the square] |
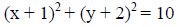 |
Center: (-1, -2)
Radius: 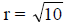
Graphing a Circle :
If the equation is in standard form, you can easily obtain the information
needed to graph the
circle. If it is not in standard form, complete the square so you can then write
it in standard form.
Example: (x – 2)^2 + (y – 3)^2 = 16
You know the center of this circle is (2, 3), so place that point on your graph
first.
You also know that the radius is 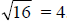 . Remember
the radius is the distance from the center
. Remember
the radius is the distance from the center
to any point on the circle. So, moving 4 units to the right from the center will
give you a point
on the circle (6, 3). Likewise , you can move 4 units to the left from the center
to obtain (-2, 3), 4
units up from the center to obtain (2, 7), and 4 units down from the center to
obtain (2, -1). You
now have four points on our circle along with the center to sketch a graph.
Example: Graphing a circle whose radius is not an integer.
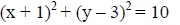
Center: (-1, 3)
Radius: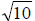
Even if the radius is not an integer, you still follow the
same process to obtain points on the
circle. Move 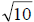 units to the right from the
center to obtain the point
units to the right from the
center to obtain the point 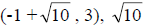 units
units
to the left from the center to obtain 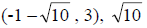 units
up from the center to obtain
units
up from the center to obtain
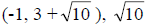 units down from the center to obtain
units down from the center to obtain
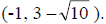
Since 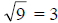 , you know that
, you know that
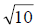 is slightly bigger than
is slightly bigger than
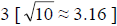 . This will help you
. This will help you
approximate the points when sketching the graph of the circle. For example, the
point
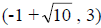 is approximately the point (-1 + 3.16, 3) =
(2.16, 3).
is approximately the point (-1 + 3.16, 3) =
(2.16, 3).
Try on your own: 1) Find the center and radius of this circle. (Answers at bottom of page)
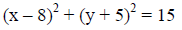
Try on your own: 2) Complete the square to get the equation into standard form.
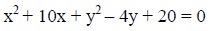
1) Center: (8, -5)
Radius: 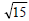
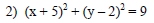
| Prev | Next |