Zeros of Polynomials

25. Start with p(x) = −6x³ + 4x² + 16x. Factor out the gcf (−2x in this case), then
use the ac- method to complete the factorization.
p(x) = −2x[3x² − 2x − 8]
p(x) = −2x[3x² − 6x + 4x − 8]
p(x) = −2x[3x(x − 2) + 4(x − 2)]
p(x) = −2x(3x + 4)(x − 2)

Set
0 = −2x(3x + 4)(x − 2)

and use the zero product property to write
−2x = 0 or 3x + 4 = 0 or x − 2 = 0.

Solving , the zeros are x = 0, −4/3, and 2.

27. Start with p(x) = −2x⁷ − 10x⁶ + 8x⁵ + 40x⁴. Factor out the gcf (−2x⁴ in this
case), then use grouping and difference of squares to complete the factorization.
p(x) = −2x⁴[x³ + 5x² − 4x − 20]
p(x) = −2x⁴[x²(x + 5) − 4(x + 5)]
p(x) = −2x⁴(x² − 4)(x + 5)
p(x) = −2x⁴(x + 2)(x − 2)(x + 5)

Set
0 = −2x⁴(x + 2)(x − 2)(x + 5)

and use the zero product property to write
−2x⁴ = 0 or x + 2 = 0 or x − 2 = 0 or x + 5 = 0.

Solving, the zeros are x = 0, −2, 2, and −5.

29. The graph of the polynomial

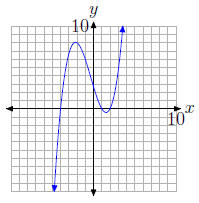
intercepts the x -axis at (−4, 0), (1, 0), and (2, 0). Hence, the zeros of the polynomial
are −4, 1, and 2.

31. The graph of the polynomial

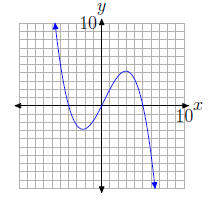
intercepts the x-axis at (−4, 0), (0, 0), and (5, 0). Hence, the zeros of the polynomial
are −4, 0, and 5.

33. The graph of the polynomial

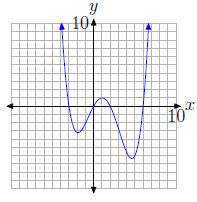
intercepts the x-axis at (−3, 0), (0, 0), (2, 0), and (6, 0). Hence, the zeros of the polynomial
are −3, 0, 2, and 6.

35. Factor p (x) = 5x³ + x² − 45x − 9 by grouping, then complete the factorization
with the difference of squares pattern .
p(x) = x²(5x + 1) − 9(5x + 1)
p(x) = (x² − 9)(5x + 1)
p(x) = (x + 3)(x − 3)(5x + 1)

Using the zero product property , the zeros are −3, 3, and −1/5. Hence, the graph
of the polynomial must intercept the x-axis at (−3, 0), (3, 0), and (−1/5, 0). Further,
the leading term of the polynomial is 5x³, so the polynomial must have the same end-behavior
as y = 5x³, namely, it must rise from negative infinity, wiggle through its
x-intercepts, then rise to positive infinity . The sketch with the appropriate zeros and
end behavior follows.

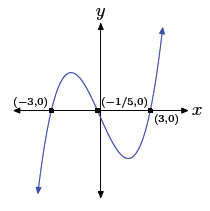
Checking on the calculator .

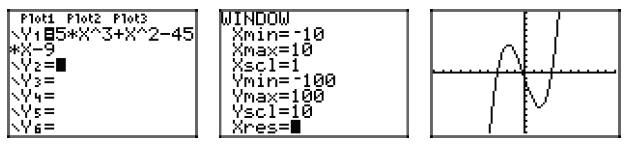
37. Factor p(x) = 4x³ − 12x² − 9x + 27 by grouping, then complete the factorization
with the difference of squares pattern.
p(x) = 4x²(x − 3) − 9(x − 3)
p(x) = (4x² − 9)(x − 3)
p(x) = (2x + 3)(2x − 3)(x − 3)

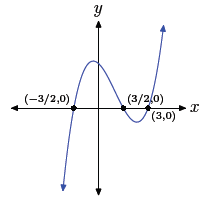
Using the zero product property, the zeros are −3/2, 3/2, and 3. Hence, the graph
of the polynomial must intercept the x-axis at (−3/2, 0), (3/2, 0), and (3, 0). Further,
the leading term of the polynomial is 4x³, so the polynomial must have the same end-behavior
as y = 4x³, namely, it must rise from negative infinity, wiggle through its
x-intercepts, then rise to positive infinity. The sketch with the appropriate zeros and
end behavior follows.

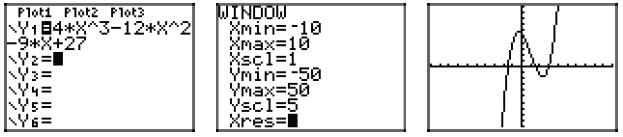
Checking on the calculator.

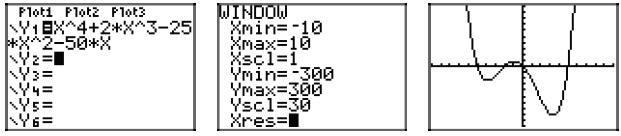
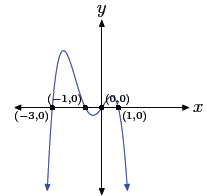
39. Start with p(x) = x⁴ + 2x³ − 25x² − 50x, then factor out the gcf (x in this case).
Then, factor by grouping and complete the factorization with the difference of squares
pattern.
p(x) = x[x³ + 2x² − 25x − 50]
p(x) = x[x²(x + 2) − 25(x + 2)]
p(x) = x(x² − 25)(x + 2)
p(x) = x(x + 5)(x − 5)(x + 2)

Using the zero product property, the zeros are 0, −5, 5, and −2. Hence, the graph of
the polynomial must intercept the x-axis at (0, 0), (−5, 0), (5, 0), and (−2, 0). Further,
the leading term of the polynomial is x⁴, so the polynomial must have the same end-behavior
as y = x⁴, namely, it must fall from positive infinity, wiggle through its
x-intercepts, then rise to positive infinity. The sketch with the appropriate zeros and
end behavior follows.

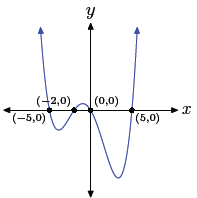
Checking on the calculator.

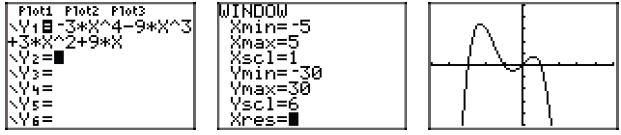
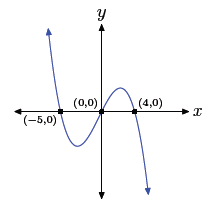
41. Start with p(x) = −3x⁴ − 9x³ + 3x² + 9x, then factor out the gcf (−3x in this
case). Then, factor by grouping and complete the factorization with the difference of
squares pattern.
p(x) = −3x[x³ + 3x² − x − 3]
p(x) = −3x[x²(x + 3) − 1(x + 3)]
p(x) = −3x(x² − 1)(x + 3)
p(x) = −3x(x + 1)(x − 1)(x + 3)

Using the zero product property, the zeros are 0, −1, 1, and −3. Hence, the graph of
the polynomial must intercept the x-axis at (0, 0), (−1, 0), (1, 0), and (−3, 0). Further,
the leading term of the polynomial is −3x⁴, so the polynomial must have the same
end-behavior as y = −3x⁴, namely, it must rise from negative infinity, wiggle through
its x-intercepts, then fall back to negative infinity . The sketch with the appropriate
zeros and end behavior follows.

Checking on the calculator.

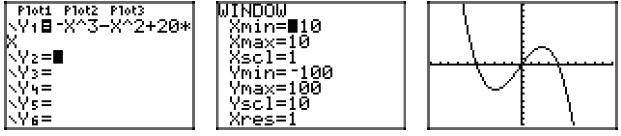
43. Start with p(x) = −x³−x²+20x, then factor out the gcf (−x in this case). Then,
complete the factorization with the ac- method .
p(x) = −x[x² + x − 20]
p(x) = −x(x + 5)(x − 4)

Using the zero product property, the zeros are 0, −5, and 4. Hence, the graph of the
polynomial must intercept the x-axis at (0, 0), (−5, 0), and (4, 0). Further, the leading
term of the polynomial is −x³, so the polynomial must have the same end-behavior as
y = −x³, namely, it must fall from positive infinity, wiggle through its x-intercepts,
then fall to negative infinity. The sketch with the appropriate zeros and end behavior
follows.

Checking on the calculator.

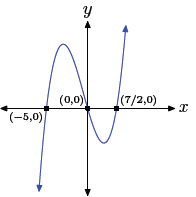
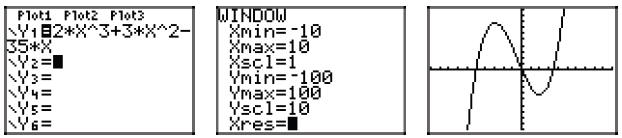
45. Start with p(x) = 2x³ +3x² −35x, then factor out the gcf (x in this case). Then,
complete the factorization with the ac-method.
p(x) = x[2x² + 3x − 35]
p(x) = x[2x² − 7x + 10x − 35]
p(x) = x[x(2x − 7) + 5(2x − 7)]
p(x) = x(x + 5)(2x − 7)

Using the zero product property, the zeros are 0, −5, and 7/2. Hence, the graph of
the polynomial must intercept the x-axis at (0, 0), (−5, 0), and (7/2, 0). Further, the
leading term of the polynomial is 2x³, so the polynomial must have the same end-behavior
as y = 2x³, namely, it must rise from negative infinity, wiggle through its
x-intercepts, then rise to positive infinity. The sketch with the appropriate zeros and
end behavior follows.

Checking on the calculator.