Thank you for visiting our site! You landed on this page because you entered a search term similar to this: greatest common factor for three number with variables.We have an extensive database of resources on greatest common factor for three number with variables. Below is one of them. If you need further help, please take a look at our software "Algebrator", a software program that can solve any algebra problem you enter!
Annotated SPSS Output
Factor Analysis
This page shows an example of a factor analysis with footnotes explaining the output. The data used in this example were collected Sidanius, who has generously shared them with us. You can download the data set here.
Overview: The "what" and "why" of factor analysis
Factor analysis is a method of data reduction. It does this by seeking underlying unobservable (latent) variables that are reflected in the observed variables (manifest variables). There are many different methods that can be used to conduct a factor analysis (such as principal axis factor, maximum likelihood, generalized least squares, unweighted least squares), There are also many different types of rotations that can be done after the initial extraction of factors, including orthogonal rotations, such as varimax and equimax, which impose the restriction that the factors cannot be correlated, and oblique rotations, such as promax, which allow the factors to be correlated with one another. You also need to determine the number of factors that you want to extract. Given the number of factor analytic techniques and options, it is not surprising that different analysts could reach very different results analyzing the same data set. However, all analysts are looking for simple structure. Simple structure is pattern of results such that each variable loads highly onto one and only one factor.
Factor analysis is a technique that requires a large sample size. Factor analysis is based on the correlation matrix of the variables involved, and correlations usually need a large sample size before they stabilize. Tabachnick and Fidell (2001, page 588) cite Comrey and Lee's (1992) advise regarding sample size: 50 cases is very poor, 100 is poor, 200 is fair, 300 is good, 500 is very good, and 1000 or more is excellent. As a rule of thumb, a bare minimum of 10 observations per variable is necessary to avoid computational difficulties.
For the example below, we are going to do a rather "plain vanilla" factor analysis. We will use iterated principal axis factor with three factors as our method of extraction, a varimax rotation, and for comparison, we will also show the promax oblique solution. The determination of the number of factors to extract should be guided by theory, but also informed by running the analysis extracting different numbers of factors and seeing which number of factors yields the most interpretable results.
In this example we have included many options, including the original and reproduced correlation matrix, the scree plot and the plot of the rotated factors. While you may not wish to use all of these options, we have included them here to aid in the explanation of the analysis. We have also created a page of annotated output for a principal components analysis that parallels this analysis. For general information regarding the similarities and differences between principal components analysis and factor analysis, see Tabachnick and Fidell (2001), for example.
factor /variables item13 item14 item15 item16 item17 item18 item19 item20 item21 item22 item23 item24 /print initial det kmo repr extraction rotation fscore /format blank(.30) /plot eigen rotation /criteria factors(3) /extraction paf /rotation varimax /method = correlation.
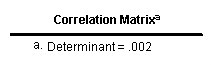
The table above is included in the output because we used the det option on the /print subcommand. All we want to see in this table is that the determinant is not 0. If the determinant is 0, then there will be computational problems with the factor analysis, and SPSS may issue a warning message or be unable to complete the factor analysis.

a. Kaiser-Meyer-Olkin Measure of Sampling Adequacy - This measure varies between 0 and 1, and values closer to 1 are better. A value of .6 is a suggested minimum.
b. Bartlett's Test of Sphericity - This tests the null hypothesis that the correlation matrix is an identity matrix. An identity matrix is matrix in which all of the diagonal elements are 1 and all off diagonal elements are 0. You want to reject this null hypothesis.
Taken together, these tests provide a minimum standard which should be passed before a factor analysis (or a principal components analysis) should be conducted.

a. Communalities - This is the proportion of each variable's variance that can be explained by the factors (e.g., the underlying latent continua). It is also noted as h2 and can be defined as the sum of squared factor loadings for the variables.
b. Initial - With principal factor axis factoring, the initial values on the diagonal of the correlation matrix are determined by the squared multiple correlation of the variable with the other variables. For example, if you regressed items 14 through 24 on item 13, the squared multiple correlation coefficient would be .564.
c. Extraction - The values in this column indicate the proportion of each variable's variance that can be explained by the retained factors. Variables with high values are well represented in the common factor space, while variables with low values are not well represented. (In this example, we don't have any particularly low values.) They are the reproduced variances from the factors that you have extracted. You can find these values on the diagonal of the reproduced correlation matrix.
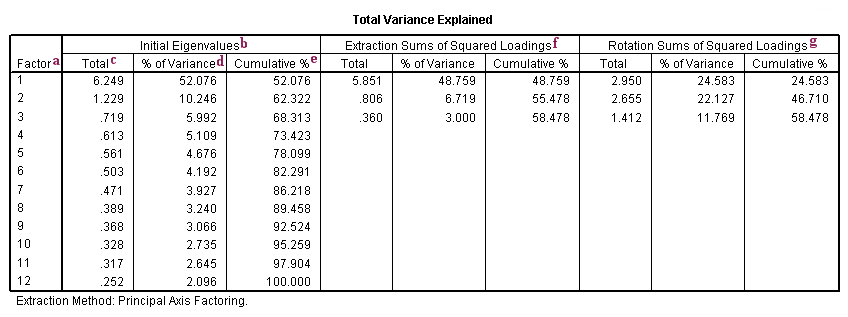
a. Factor - The initial number of factors is the same as the number of variables used in the factor analysis. However, not all 12 factors will be retained. In this example, only the first three factors will be retained (as we requested).
b. Initial Eigenvalues - Eigenvalues are the variances of the factors. Because we conducted our factor analysis on the correlation matrix, the variables are standardized, which means that the each variable has a variance of 1, and the total variance is equal to the number of variables used in the analysis, in this case, 12.
c. Total - This column contains the eigenvalues. The first factor will always account for the most variance (and hence have the highest eigenvalue), and the next factor will account for as much of the left over variance as it can, and so on. Hence, each successive factor will account for less and less variance.
d. % of Variance - This column contains the percent of total variance accounted for by each factor.
e. Cumulative % - This column contains the cumulative percentage of variance accounted for by the current and all preceding factors. For example, the third row shows a value of 68.313. This means that the first three factors together account for 68.313% of the total variance.
f. Extraction Sums of Squared Loadings - The number of rows in this panel of the table correspond to the number of factors retained. In this example, we requested that three factors be retained, so there are three rows, one for each retained factor. The values in this panel of the table are calculated in the same way as the values in the left panel, except that here the values are based on the common variance. The values in this panel of the table will always be lower than the values in the left panel of the table, because they are based on the common variance, which is always smaller than the total variance.
g. Rotation Sums of Squared Loadings - The values in this panel of the table represent the distribution of the variance after the varimax rotation. Varimax rotation tries to maximize the variance of each of the factors, so the total amount of variance accounted for is redistributed over the three extracted factors.
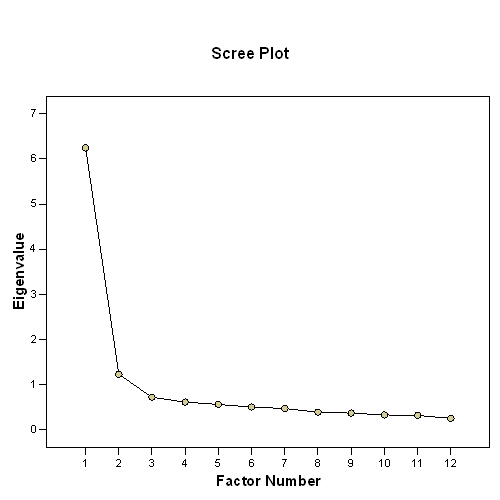
The scree plot graphs the eigenvalue against the factor number. You can see these values in the first two columns of the table immediately above. From the third factor on, you can see that the line is almost flat, meaning the each successive factor is accounting for smaller and smaller amounts of the total variance.
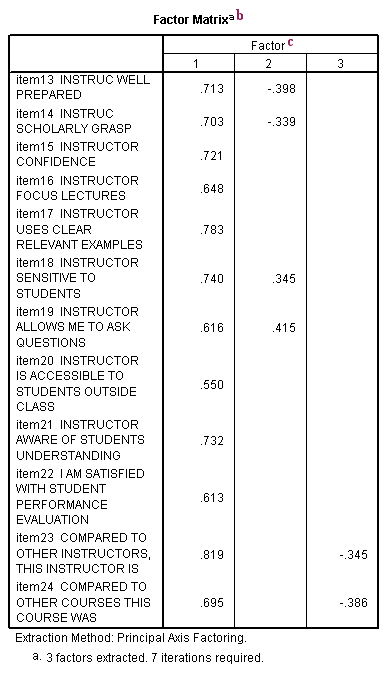
b. Factor Matrix - This table contains the unrotated factor loadings, which are the correlations between the variable and the factor. Because these are correlations, possible values range from -1 to +1. On the /format subcommand, we used the option blank(.30), which tells SPSS not to print any of the correlations that are .3 or less. This makes the output easier to read by removing the clutter of low correlations that are probably not meaningful anyway.
c. Factor - The columns under this heading are the unrotated factors that have been extracted. As you can see by the footnote provided by SPSS (a.), three factors were extracted (the three factors that we requested).
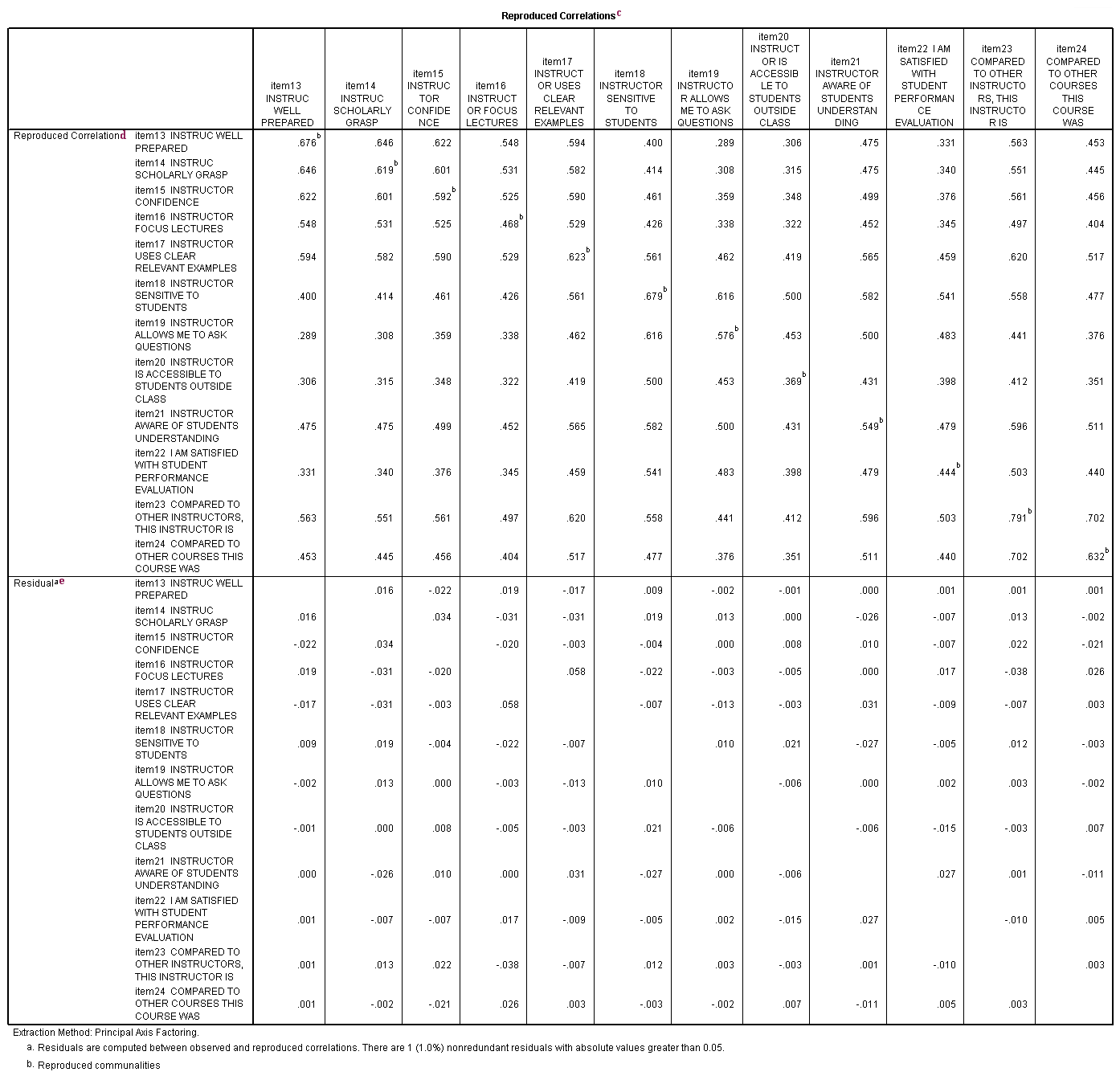
c. Reproduced Correlations - This table contains two tables, the reproduced correlations in the top part of the table, and the residuals in the bottom part of the table.
d. Reproduced Correlation - The reproduced correlation matrix is the correlation matrix based on the extracted factors. You want the values in the reproduced matrix to be as close to the values in the original correlation matrix as possible. This means that the residual matrix, which contains the differences between the original and the reproduced matrix to be close to zero. If the reproduced matrix is very similar to the original correlation matrix, then you know that the factors that were extracted accounted for a great deal of the variance in the original correlation matrix, and these few factors do a good job of representing the original data. The numbers on the diagonal of the reproduced correlation matrix are presented in the Communalities table in the column labeled Extracted.
e. Residual - As noted in the first footnote provided by SPSS (a.), the values in this part of the table represent the differences between original correlations (shown in the correlation table at the beginning of the output) and the reproduced correlations, which are shown in the top part of this table. For example, the original correlation between item13 and item14 is .661, and the reproduced correlation between these two variables is .646. The residual is .016 = .661 - .646 (with some rounding error).
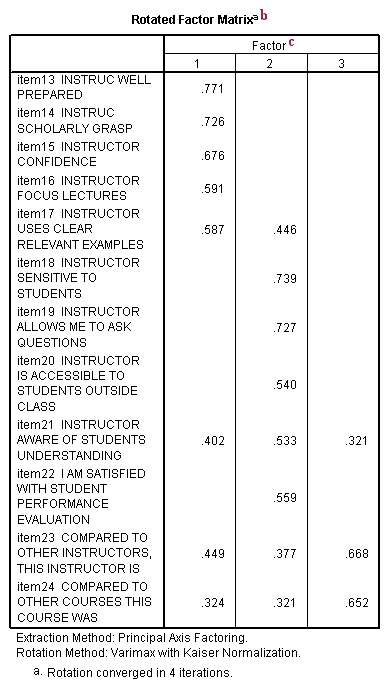
b. Rotated Factor Matrix - This table contains the rotated factor loadings, which are the correlations between the variable and the factor. Because these are correlations, possible values range from -1 to +1. On the /format subcommand, we used the option blank(.30), which tells SPSS not to print any of the correlations that are .3 or less. This makes the output easier to read by removing the clutter of low correlations that are probably not meaningful anyway.
c. Factor - The columns under this heading are the rotated factors that have been extracted. As you can see by the footnote provided by SPSS (a.), three factors were extracted (the three factors that we requested). These are the factors that analysts are most interested in and try to name. For example, the first factor might be called "instructor competence" because items like "instructor well prepare" and "instructor competence" load highly on it. The second factor might be called "relating to students" because items like "instructor is sensitive to students" and "instructor allows me to ask questions" load highly on it. The third factor has to do with comparisons to other instructors and courses.
The table below is from another run of the factor analysis program shown above, except with a promax rotation. We have included it here to show how different the rotated solutions can be, and to better illustrate what is meant by simple structure. As you can see with an oblique rotation, such as a promax rotation, the factors are permitted to be correlated with one another. With an orthogonal rotation, such as the varimax shown above, the factors are not permitted to be correlated (they are orthogonal to one another). Oblique rotations, such as promax, produce both factor pattern and factor structure matrices. For orthogonal rotations, such as varimax and equimax, the factor structure and the factor pattern matrices are the same. The factor structure matrix represent the correlations between the variables and the factors and is often called the factor loading matrix. The factor pattern matrix represents the linear combination of the variables.
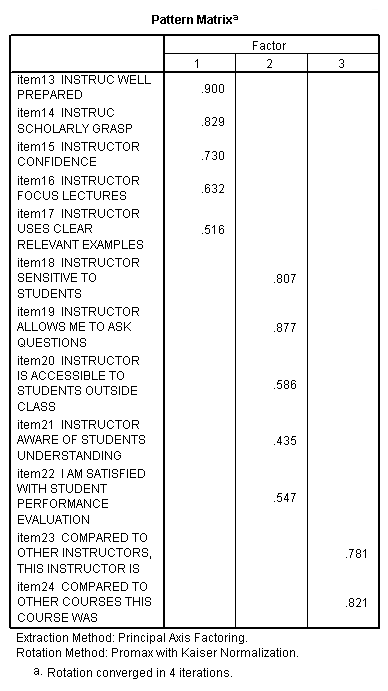
The table below indicates that the rotation done is an oblique rotation. If an orthogonal rotation had been done (like the varimax rotation shown above), this table would not appear in the output because the correlations between the factors are set to 0. Here, you can see that the factors are highly correlated.

The rest of the output shown below is part of the output generated by the SPSS syntax shown at the beginning of this page.

a. Factor Transformation Matrix - This is the matrix by which you multiply the unrotated factor matrix to get the rotated factor matrix.
The plot above shows the items (variables) in the rotated factor space. While this picture may not be particularly helpful, when you get this graph in the SPSS output, you can interactively rotate it. This may help you to see how the items (variables) are organized in the common factor space.
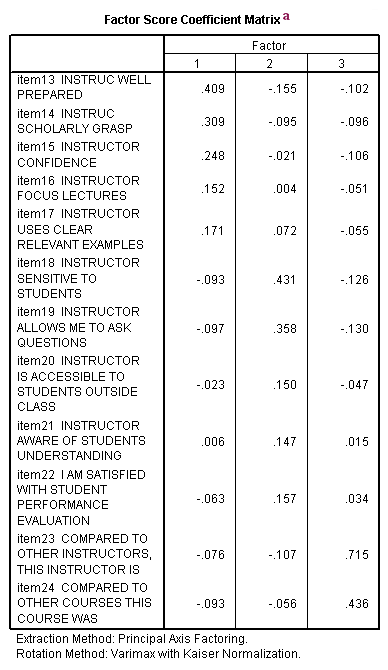
a. Factor Score Coefficient Matrix - This is the factor weight matrix and is used to compute the factor scores.

a. Factor Score Covariance Matrix - Because we used an orthogonal rotation, this should be a diagonal matrix, meaning that the same number should appear in all three places along the diagonal. In actuality the factors are uncorrelated; however, because factor scores are estimated there may be slight correlations among the factor scores.
Report an error on this page
UCLA Researchers are invited to our Statistical Consulting Services
We recommend others to our list of Other Resources for Statistical Computing Help
These pages are Copyrighted (c) by UCLA Academic Technology Services
The content of this web site should not be construed as an endorsement of any particular web site, book, or software product by the University of California