| Frequently Asked Questions About the Core-Plus Mathematics Project 21 September 2005 Click on a link below to jump to a particular question.
Characteristics of the CPMP Curriculum (print only this topic here) In the Classroom (print only this topic here) - Should the Core-Plus Mathematics Project curriculum be used with heterogeneous or homogeneous classroom groupings of students?
- Can the Core-Plus Mathematics Project curriculum be used with students having limited English proficiency (LEP), or with English language learners (ELL)?
Student Preparation (print only this topic here) Evaluation Evidence (print only this topic here) Local Implementation (print only this topic here) External resources and contact information for general mathematics reform issues
Characteristics of the CPMP Curriculum
| | Q | How is the Core-Plus Mathematics Project curriculum different from traditional US mathematics curricula? | | A | One way to characterize the CPMP curriculum, in contrast to traditional curricula, is to see it as an effort to achieve a better balance among skills, conceptual understanding, and problem solving. This can be summarized as follows: | | | | Traditional Approach | CPMP Approach | | Instructional Focus | facts and procedures, with some applications and problem solving | conceptual understanding, problem solving, mathematics done in context, with requisite work on procedures and facts | | Method | direct instruction, memorize and practice, with some projects and occasional group activities | active student engagement in inquiry and investigation, guided by probing teacher questions, with teacher-led introductions and summaries, and some direct instruction | | Supplementary Material | problem solving, applications, thinking skills | additional skill practice | | | | The prevalence and disappointing consequences of the traditional approach in the US are verified by international comparisons such as the Third International Mathematics and Science Study. |
| Q | How is the final version of the Core-Plus Mathematics Project curriculum different from the pilot-test version? | | A | There are several differences between the pilot-test version and the final version of the CPMP curriculum. These differences came about based on the four-year research, development, and evaluation cycle used for each course: | | | | Year 1 | initial development, in consultation with teachers, content and instructional specialists, and an international advisory board, including some small-scale local tryouts | | Year 2 | pilot testing in 19 Michigan schools, followed by revision based on feedback from the pilot-test teachers, consultants, advisory board, and data collected on the pilot test | | Year 3 | field testing in 36 schools around the country, followed by revision based on feedback from the field-test teachers, consultants, advisory board, and data collected on the field test | | Year 4 | final revisions and publication | | | | Based on feedback and data from this development process, the basic approach of the curriculum was maintained, but many changes were made from the pilot version to the final published version. These changes varied from minor rewording of questions to major reorganization of units. More practice with algebra skills was added as were structured reviews (see the next two questions for specifics). |
| Q | Is the attention to algebraic skills in the Core-Plus Mathematics Project curriculum as thorough as that in a traditional algebra program? | | A | Yes and no. Yes, the CPMP curriculum carefully and thoroughly develops algebraic skills. However, there are many important skills and concepts that students need to learn, and a limited amount of instructional time. Thus, choices had to be made about what to include, what to emphasize, and what to delete. Some particularly complex and little-used algebraic skills, which may be included in some traditional algebra programs, like simplifying complicated rational and radical expressions, are not included in the CPMP curriculum. On the other hand, vital algebraic skills, like factoring, finding equivalent expressions, and solving equations, are covered thoroughly. CPMP developers devoted considerable time and effort designing the curriculum so that these skills are developed meaningfully and completely, based on solid conceptual understanding and appropriate practice. The developers learned from the pilot and field testing, and from the field-test evaluation research, that progress was being made towards achieving these goals. However, it was also found that more practice with algebraic skills was needed. So the following modifications and additions were made: | | | - Short skill maintenance sheets now are provided for each unit (chapter), beginning with Unit 4 of Course 1, as part of the Teacher Resource materials. Most teachers assign these as homework and then discuss them in class.
- New lessons and exercises involving symbolic reasoning strategies and algebra practice were added to the student materials for Courses 1-3, particularly in Course 3.
- In Course 4, the primary algebra focus is on symbolic reasoning and manipulation strategies needed for calculus. The heavy emphasis on symbolic reasoning and manipulation skills in Course 4 is consistent with the original development plan. Throughout the entire curriculum, algebraic concepts and methods are developed using verbal, graphic, numeric, and symbolic representations. In Course 1, there is more emphasis on reasoning with verbal, graphic, and numeric representations, and less emphasis on symbolic manipulation. By-hand symbolic manipulation becomes more prominent as the courses progress, so that by Course 4 symbolic reasoning and manipulation is the primary focus. The reasons for using this gradual approach to teaching and learning symbolic reasoning and manipulation skills are: (a) it allows the symbolic skills to be learned based on solid conceptual understanding and with well-understood links to graphs and tables, and (b) it delays the heavy algebraic skill work to a point closer to when some students will actually need this facility, i.e., college mathematics.
- A set of algebraic skill practice problems has been added at the end of each lesson in Course 4, specifically to ensure a smooth transition to college mathematics and college math placement exams.
| | | CPMP developers continue to work with teachers using the curriculum to identify other adjustments and/or supplements that might be needed. For example, a Reference and Practice book has been developed for each course. These books provide an "executive summary" of the main ideas of the preceding course, and also sets of mixed review and skill-practice exercises. |
| Q | How are summaries and review provided in the Core-Plus Mathematics Project curriculum? | | A | It is crucial that students summarize and review what they have learned. Students summarize and review in the CPMP curriculum in the following ways: | | - There is a set of boxed-off review questions at the end of every investigation (1-3 days). The teacher leads a whole-class discussion of these "Checkpoint" questions, making sure all students understand the main ideas.
- Students create summaries of important ideas, definitions, and methods in a structured section of their notes called a "math toolkit." They make entries into this toolkit based on specific prompts from their teacher suggested in the teacher notes. The math toolkits become, in essence, student-created glossaries.
- There is a summary and review lesson at the end of every unit (3-6 weeks). These are called Looking Back lessons. A Looking Back lesson consists of tasks that summarize and review all the main ideas of the unit.
- The short skill maintenance sheets which are part of the Teacher Resource materials for each unit, beginning with Unit 4 of Course 1, provide periodic review of material from previous units and courses.
- Also, at the end of each Course 4 unit, students are given an outline of a unit summary. Students complete this as a record of the concepts, facts, and procedures that they have learned. As well as being an excellent summary and review, these concise summaries can be kept for easy reference later on.
- At the end of each course, there is a 1-2 week synthesizing unit, called a Capstone. The Capstone unit is designed to pull together and review what students have learned during the year. Each Capstone involves investigating problem situations related to one context or one theme. For example, the Course 1 Capstone unit is about putting on a school carnival, including games, finances, and planning, and the Course 3 Capstone is centered around the theme of optimization.
- Of course, homework, quizzes, projects, and tests also contribute to review and summary.
| | | The math toolkits and the maintenance sheets were incorporated into the final version of the curriculum as part of the development process (they were not part of the pilot-test version). These modifications were made to enable students to better organize, summarize, review, and retrieve the important mathematical concepts, principles, and methods that they have studied. |
| Q | Are there worked-out examples in the Core-Plus Mathematics Project curriculum? | | A | Yes, there are many worked-out examples in the CPMP curriculum. And it is the students who work them out! Through carefully orchestrated investigations, the students produce a large number of worked examples. Students learn better when they do the work, instead of (possibly) reading examples worked out by textbook authors. |
In the Classroom
| | Q | Should the Core-Plus Mathematics Project curriculum be used with heterogeneous or homogeneous classroom groupings of students? | | A | The CPMP curriculum is a flexible curriculum that can be used in a variety of ways with different groupings of students. Thus, each school should make the decision about grouping students that best fits their student body and community. In whatever configuration the school chooses, the availability of extension activities in the student text, and of maintenance tasks in the Teacher Resource materials, as well as different styles of practice problems, allows teachers to provide appropriate challenge or review for each student. At this time, the CPMP curriculum is being successfully used in math/science magnet schools, in high schools with heterogeneous classrooms, with accelerated 8th graders, in accelerated tracks that move more quickly through the materials starting in 9th grade, and in schools that use several different curricula. In many schools, the CPMP materials are used successfully with all the students, whether they are tracked or untracked. |
| Q | Can the Core-Plus Mathematics Project curriculum be used with students having limited English proficiency (LEP), or with English language learners (ELL)? | | A | Bill Bokesch was a Core-Plus field-test teacher in a southern California high school. Over 70% of the students in his school did not have English as their first language. In a recent article in MathLink, Bill described the techniques he learned in a 45-hour Professional Development course required by the California legislature to help teachers teach LEP and ELL students who are assigned to regular instructional classes (as all California students are now). The course is called "Specially Designed Academic Instruction in English" (SDAIE). Bill compared the SDAIE recommendations with what he was already doing as a CMIC teacher. | SDAIE Recommends | CMIC Incorporates | | Vary the settings in which students learn. | Bill's students work in groups of two, three, or four, or work individually, depending on the class activity. They also have whole-class discussions. | | Call on students' existing knowledge, observations, and experience. | The "Think About This Situation," which launches each CMIC lesson allows students to have informal verbal interaction during class. At this time they make connections between their everyday experiences, their previous knowledge, and the new mathematical concepts they are meeting. | | Make the most of recurring problems and mathematical experiences. | Problems that students encounter in CMIC lessons, such as finding rates of change, reappear in deeper and more complex forms as students progress through the curriculum. Because they are familiar with such problems, students have the vocabulary, confidence and past knowledge to discuss the problems at increasing levels of difficulty. | | Require students to learn through hands-on investigation. | Bill notes that the work his Course 4 students are doing with navigation uses authentic problems similar to those he handled in the U.S. Navy. Working with authentic tools and problems, and with peer interaction, helps students develop language skills as well as mathematical understanding. | | Emphasize how students' mathematics and language skills will benefit them in the future. | CMIC materials help Bill emphasize a key question "What is 'the real world'?" Career Day speakers from local businesses reinforce the idea that modern employers need workers who can think for themselves and work with others toward the goals of the company. | | Work as a whole group to understand new concepts and vocabulary. | By using whole class discussion for the "Think About This Situation" lesson introduction, CMIC students are able to gain the vocabulary and concepts they need to finish the investigations and MORE problems in groups or on their own. | | Integrate technology. | Use of the graphing calculator in CMIC lessons provides a bridge over language-related or cultural barriers. Calculators provide visual images that help students understand problems and express solutions. | Bill concludes: "By using appropriate settings, discussion, investigation, and tools, I help students in my CMIC classes learn mathematics in a way that strengthens their language skills and allows them to build on their existing mathematics knowledge." To read Bill Bokesch's entire article, download ELL-LEP.pdf (58 kb). |
Student Preparation
| | Q | Are the topics recommended by the College Board as preparation for Advanced Placement Calculus covered in the Core-Plus Mathematics curriculum? | | A | Yes, all of the topics for Algebra and Trigonometry, for Geometry, and for Coordinate Geometry are developed in the CPMP four-course curriculum. In some cases, topics appear in multiple courses. For a list of all topics recommended by the College Board, including Graphing Calculators and Other Topics, and corresponding page references in CPMP Courses 1-4, download this printable PDF file. |
| Q | When should students who are taught using the Core-Plus Mathematics Project curriculum take AP Calculus and AP Statistics? | | A | After completing three years of the CPMP curriculum, students are very well prepared to take AP Statistics. Some schools are finding that one semester is enough to teach the statistics in the AP syllabus that had not already been learned in the first three CPMP courses.
After completing four years of the CPMP curriculum, students are very well prepared to take AP Calculus. (See District Reports for AP results from some schools using the published CPMP curriculum, Contemporary Mathematics in Context.) Just as in a traditional four-year curriculum (Algebra-Geometry-Advanced Algebra-Precalculus), some form of acceleration is needed for students who want to take calculus as seniors. The second question in the section on Local Implementation questions identifies several acceleration options that schools have used successfully to enable students to complete the four years of the CPMP curriculum prior to their senior year. |
| Q | Does the Core-Plus Mathematics Project curriculum prepare students for college? | | A | Yes. Evaluation research has shown that students using the field-test version of the CPMP curriculum do as well as, or better than, non-CPMP students on the SAT and ACT college entrance exams. Also, a study at the University of Michigan of two Michigan high schools found that in collegiate mathematics courses at the University of Michigan, graduates of the CPMP program performed as well, or better than, graduates of a traditional mathematics curriculum. Finally, students completing pilot and field-test versions of the CPMP curriculum have been accepted at over 450 schools around the country, including Harvard University, Stanford, Duke University, Massachusetts Institute of Technology (MIT), Notre Dame, the University of Michigan, the University of Chicago, the University of California at Berkeley, Clemson University, the University of Virginia, Purdue University, Boston College, the University of Wisconsin - Madison, Rice University, the University of Washington, Georgetown University, the Air Force Academy, Northwestern University, Morehouse College, the University of Arizona, Vanderbilt University, the University of Hawaii, and Pennsylvania State University. Students who study the final published version of the CPMP curriculum should be even better prepared for college.
(Other indicators of preparedness for college based on SAT, ACT, and AP Calculus and AP Statistics from schools using the published version of Core-Plus Mathematics are reported at District Reports.) |
| Q | Does the Core-Plus Mathematics Project curriculum provide the mathematics necessary to be successful on traditional college math placement exams? | | A | Yes. In particular, there is a set of skill practice problems at the end of every lesson in Course 4. These problem sets are designed to provide practice on the specific types of problems that are often found on college math placement exams. As with any curriculum, the students' degree of preparation will depend on their own efforts. |
Evaluation Evidence
For more information on evaluation evidence, see the Evaluation page and the annotated list of Research Publications. | | Q | What do evaluation studies say about the effectiveness of the Core-Plus Mathematics Project curriculum? | | A | There is a large and growing body of rigorous research documenting the effectiveness of the CPMP curriculum. Based on evidence from nationally standardized tests (ITED, SAT, ACT, NAEP), course-specific tests, researcher-developed tests, interviews, and surveys, the CPMP curriculum has been shown to enhance students' mathematical achievement and attitudes toward mathematics. Quantitative Thinking
CPMP students outperform comparison students on the mathematics subtest of the nationally standardized Iowa Tests of Educational Development ITED-Q. Conceptual Understanding
CPMP students demonstrate better conceptual understanding than students in more traditional curricula. Problem Solving Ability
CPMP students demonstrate better problem solving ability than comparison students. Applications and Mathematical Modeling
CPMP students are better able to apply mathematics than students in more traditional curricula. Algebraic Reasoning
CPMP students perform better on tasks of algebraic reasoning than comparison students. Algebraic Procedural Skills
This is the one area for which field-test research indicates mixed results. On some evaluation tests, CPMP students do as well or better, on others they do less well than comparison students. As part of the curriculum development process, revisions have been made to strengthen students' algebraic skills. The final and published version of the Core-Plus Mathematics curriculum maintains the well-documented effectiveness of the curriculum, while strengthening students' algebraic procedural skills. Important Mathematics in Addition to Algebra and Geometry
CPMP students perform well on mathematical tasks involving probability, statistics, and discrete mathematics. National Assessment of Educational Progress (NAEP)
CPMP students scored well above national norms on a test comprised of released items from the National Assessment of Educational Progress. Student Perceptions and Attitudes
CPMP students have better attitudes and perceptions about mathematics than students in more traditional curricula. Performance on State Assessments
The pass rate on the 2004-05 Tenth-Grade Washington Assessment of Student Learning Mathematics test for 22 state of Washington high schools that were in at least their second year using the Core-Plus Mathematics curriculum was significantly higher than that of a sample of 22 schools carefully matched on prior mathematics achievement, percent of students from low-income families, percent of underrepresented minorities, and student enrollment. College Entrance Exams - SAT and ACT
CPMP students do as well as, or better than, comparable students in more traditional curricula on the SAT and ACT college entrance exams. Performance on College Math Placement Tests
On a mathematics department placement test used at a major midwestern university, CPMP students performed as well as students in traditional precalculus courses on basic algebra and advanced algebra subtests, and they performed better on the calculus readiness subtest. Performance in College Mathematics Courses
CPMP students completing the four-year curriculum perform as well as, or better than, comparable students in a more traditional curriculum in college mathematics courses at the calculus level and above. The above results are drawn from several sources, including two research papers presented at the 1998 Annual Meeting of the American Educational Research Association:
- An Emerging Profile of the Mathematical Achievement of Students in the Core-Plus Mathematics Project
- Students' Perceptions and Attitudes in a Standards-based High School Mathematics Curriculum,
two field-test progress reports: - Mathematical Achievement on Standardized Tests
- Assessments of Students' Mathematical Performance,
and a paper appearing in the Journal for Research in Mathematics Education, "Effects of Standards-based Mathematics Education: A Study of the Core-Plus Mathematics Project Algebra/Functions Strand," Vol. 31, No. 3 (2000). |
| Q | How well do Core-Plus students perform on standardized tests like the Iowa Tests of Educational Development? | | A | On the quantitative section of the Iowa Tests of Educational Development (ITED-Q), Core-Plus students significantly outperformed both the nationally representative norm group and comparison students in the same school who had a traditional mathematics curriculum. The Ability to Do Quantitative Thinking (ITED-Q or ATDQT) is the mathematical subtest of the Iowa Test of Educational Development, a nationally standardized battery of high school tests. The ITED-Q is a 40-item multiple-choice test with the primary objective of measuring students' ability to employ appropriate mathematical reasoning in situations requiring the interpretation of numerical data and charts or graphs that represent information related to business, social and political issues, medicine, and science. The ITED-Q administered in CPMP national field test schools at the beginning of Course 1 served as the pretest for all courses, so the pretest-posttest analyses for Courses 1, 2, and 3 are for one, two, and three years of mathematics instruction, respectively. For the first and second years, there was a comparison group of ninth- or tenth-grade students in traditional mathematics courses in some field-test schools with both curricula. Results for the following three cohort groups of CPMP students were analyzed: (1) all students who completed both the Course 1 Pretest and the Course 1 Posttest, (2) all students who completed both the Course 1 Pretest and the Course 2 Posttest, and (3) all students who completed both the Course 1 Pretest and the Course 3 Posttest. Table 1 below gives median (middle) ITED-Q percentiles of the CPMP and comparison distributions. Table 1
| CPMP Students | Comparison Students | | N | Median | N | Median | Course 1 Pretest
Course 1 Posttest | 2,944
2,944 | 54
62 | 527
527 | 54
55 | Course 1 Pretest
Course 2 Posttest | 2,270
2,270 | 59
66 | 201
201 | 59
62 | Course 1 Pretest
Course 3 Posttest | 1,457
1,457 | 65
71 | | | The results given in Table 1 are illustrated in the following graph. 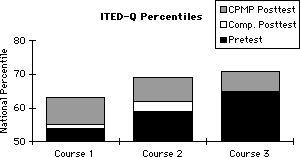 Pretest to posttest growth in percentiles indicates growth by CPMP students beyond that of the national norm group. Such increases appear consistently across the CPMP distribution for each year. For example, the median CPMP Course 1 student increased the equivalent of nearly two years in just one year's time. Allowing for pretest differences, CPMP posttest means in schools with comparison groups are significantly greater than those of the comparison students. |
| Q | How well do Core-Plus students perform on the SAT? | | A | On the SAT-I Mathematics test, students completing Core-Plus mathematics field-test courses performed at least as well as students in traditional mathematics curricula. SAT data for 1997 from 13 CPMP schools were separated into groups according to the secondary mathematics courses the students had completed. SAT Mathematics scores of students who had completed Courses 1, 2 and 3 were compared to students who completed traditional algebra, geometry and advanced algebra. In Table 1, these groups are labeled "CPMP 3" and "Advanced Algebra," respectively. The CPMP 3 average (mean) is greater than that of the Advanced Algebra students, but the difference is not significant at the 0.05 level. Table 1: Means and Standard Deviations of 1997 SAT Mathematics Scores
| CPMP3 | Advanced Algebra | | Number of Students | Average | Number of Students | Average | | 371 | 552.0 | 190 | 543.4 | In one field-test school at the beginning of the CPMP field test (Fall 1994), all ninth-grade students who qualified for pre-algebra or algebra were randomly assigned by computer to CPMP Course 1 or to a traditional course. Many of these students completed Advanced Algebra or CPMP Course 3 in their junior year and took the SAT either in spring or summer of their junior year or in fall of their senior year. As shown in Table 2, the average Grade 8 ITBS Mathematics scores are nearly identical for the CPMP students and those in the traditional curriculum. Thus, these two groups were well-matched on mathematical achievement prior to high school. They learned mathematics in the same school and sometimes from some of the same teachers. The only apparent systematic difference between the groups is the curriculum. The average SAT Math score for the CPMP group is greater than that of the traditional group, but the difference is not statistically significant at the 0.05 level. Table 2: ITBS Math and SAT Math Means and Standard Deviations for CPMP and Well-Matched Traditional Students in One High School
| Grade 8 ITBS Math Percentile | SAT Math | | Group | Number of Students | Average | Average | | CPMP | 54 | 57.1 | 484.6 | | Traditional | 44 | 57.5 | 467.0 | The results in Tables 1 and 2 are illustrated in the following graph. 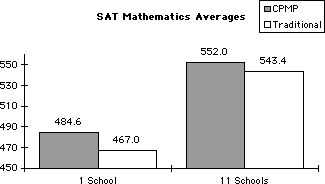 |
| Q | How well do Core-Plus students perform on the ACT? | | A | On the ACT Mathematics test, students completing Core-Plus mathematics field-test courses performed as well as students in traditional mathematics curricula. The 2,944 CPMP and 527 traditional students in the original CPMP field-test sample had nearly identical average scores on the ITED-Q pretest administered at the beginning of Grade 9. ACT scores were available from a reasonably large subset of these students, and their average ACT Mathematics and ACT Composite scores are given in Table 1. There is no significant difference (0.05 level) between the CPMP and traditional averages (means) for either the Mathematics or Composite score. Table 1
| ACT Mathematics | ACT Composite | | Group | Number of Students | Average | Average | | CPMP | 531 | 19.2 | 20.4 | | Traditional | 111 | 19.8 | 20.3 | In one school district at the beginning of the CPMP field test (Fall 1994), all ninth-grade students in the two CPMP field-test schools who qualified for remedial mathematics through algebra were randomly assigned by computer to CPMP Course 1 or to the appropriate traditional course. Many of these students completed Advanced Algebra or CPMP Course 3 in their junior year and took the ACT either in spring or summer of their junior year or in fall of their senior year. The average sixth-grade CAT Mathematics percentiles for the CPMP students and those in the traditional curriculum are similar as shown in Table 2, so these two groups were well-matched on mathematical achievement prior to high school. They learned mathematics in the same schools and sometimes from some of the same teachers. The only apparent systematic difference was the curriculum. For this set of students, the average ACT Math scores for the CPMP group is almost identical to that of the traditional group. The average ACT Composite score for the CPMP group is greater than that of the traditional group, but the difference is not statistically significant at the 0.05 level. Table 2
| CAT Math Percentile | ACT Mathematics | ACT Composite | | Group | Number of Students | Average | Average | Average | | CPMP | 71 | 66.3 | 18.3 | 20.3 | | Traditional | 42 | 68.5 | 18.4 | 19.1 | The results in Tables 1 and 2 are illustrated in the following graph. 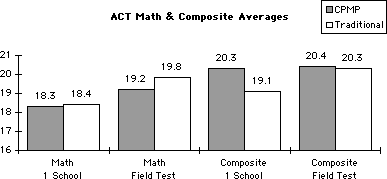 |
| Q | How well do Core-Plus students perform on mathematics placement tests at the college level? | | A | On a Mathematics Department Placement Test from a large Midwestern university, students completing field-test versions of Core-Plus Mathematics Courses 1-3 plus the precalculus path of Course 4 performed as well as students in traditional precalculus on basic algebra and advanced algebra subtests and better on the calculus readiness subtest. The Mathematics Placement Test, compiled from a bank of items developed by the Mathematical Association of America, that is presently used at a major university was administered in several field-test schools in May 1999 at the end of CPMP Course 4 and traditional Precalculus courses. This test contains three subtests - Basic Algebra (15 items), Advanced Algebra (15 items) and Calculus Readiness (20 items). The first two subtests consist almost entirely of algebraic symbol manipulation, and the third subtest measures some of the important concepts that underlie calculus. A graphing calculator (with no symbol manipulation capability) is allowed on this test. The CPMP Course 4 students included in the comparison below are all those in the 1998-99 Course 4 field test who completed the 6-unit "preparation for calculus" path as the last course in their sequence of CPMP Courses 1-4 (N = 164). The Precalculus students, also from field-test schools, completed a traditional precalculus course following a sequence of Algebra, Geometry and Advanced Algebra (N = 177). The two groups were further restricted to those students who indicated on a written survey their intention to attend a four-year college or university in the next school year. Eighth-grade mathematics standardized test scores for both groups were, on average, at about the 85th national percentile. Means by group and subtest are plotted in Figure 1. The CPMP Course 4 mean was significantly (p Figure 1: 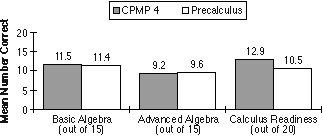 The Mathematics Department at the university that provided this placement test combines the subtest scores by a formula to recommend enrollment for each student in one of four college mathematics courses - Calculus I, Precalculus, Intermediate Algebra, and Beginning Algebra. Using that formula, the percent of CPMP Course 4 and Precalculus students who would be recommended for each course is illustrated in Figure 2. A much higher percentage of CPMP Course 4 students (50.6%) than traditional Precalculus students (39.0%) would be recommended for Calculus I suggesting that the CPMP curriculum with this sequence of Course 4 units better prepares students for this examination and presumably for college calculus. Figure 2: 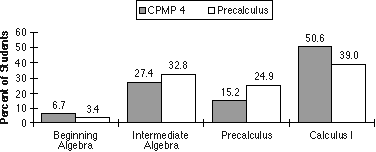 |
| Q | How well do Core-Plus students perform in college mathematics courses? | | A | CPMP Course 4 was field tested nationally during the 1998-99 school year and some preliminary evidence on how CPMP graduates perform in collegiate mathematics courses is beginning to appear. A study completed at the University of Michigan examined the performance of students from two Michigan high schools in the same district, Andover High School and Lahser High School. In 1995 and 1996, a traditional mathematics curriculum was in place at both schools, and Lahser continued to use their traditional curriculum through 1998-99. In 1997, all Andover students who had not previously been accelerated had studied the CPMP curriculum, and by 1998 all Andover students were in the CPMP program. Computer files provided by the University of Michigan registrar were used to generate the achievement data summarized in the following table. The table includes the number of matriculants from the school under the year, the mathematics courses taken in the first year of study at the University of Michigan together with the grade point averages, and numbers of elections and the course averages in each year. The mathematics courses are 105/110 (precalculus), 115 (calculus I), 116 (calculus II), 215 (calculus III), 216 (introduction to differential equations), and honors (all honors math courses open to freshmen). The grade point averages were calculated using the University of Michigan system as follows: A+ (4.3), A (4), A- (3.7), B+ (3.3), B (3), ..., D (1), D- (0.7), E+ 0.3), and E (0). Table 1: Mean Grade Point Averages (Number of Students) by School, Course, and Year
| Andover High School | Lahser High School | | College Class | 1995
(50) | 1996
(74) | 1997
(87) | 1998
(72) | 1995
(34) | 1996
(57) | 1997
(45) | 1998
(35) | | 105 | 3.18(4) | 2.29(6) | 2.74(13) | 2.98(6) | 1.46(7) | 3(4) | 2.60(5) | 2.97(3) | | 115 | 2.86(14) | 2.60(19) | 3.08(32) | 2.89(25) | 2.33(7) | 2.82(13) | 2.58(15) | 2.87(7) | | 116 | 2.67(14) | 3.33(12) | 3.17(19) | 3.49(12) | 2.45(6) | 3.21(18) | 2.63(8) | 2.29(8) | | 215 | 2.66(5) | 3.10(4) | 2.95(6) | 2.99(8) | 2.50(2) | 3.17(11) | 3.34(6) | 2.34(5) | | 216 | 2.15(2) | 4(1) | 4(2) | 3.30(2) | --- | 3.67(3) | 3.65(2) | --- | | Honors | --- | 3.28(5) | --- | --- | 3.30(1) | 3.77(3) | 4.23(4) | --- | | All Courses | 2.76(39) | 2.89(47) | 3.06(72) | 3.07(53) | 2.15(23) | 3.15(52) | 2.92(40) | 2.57(23) | The Andover achievement for the years 1997 and 1998 when CPMP was in place is stronger than both pre-CPMP Andover (i.e., 1995 and 1996) and 1997 and 1998 Lahser achievement. Similarly, the number of Andover matriculants at the University of Michigan for the last two years is greater than that for the previous two years. These achievement and admissions data clearly support the view that in collegiate mathematics courses at the University of Michigan, graduates of the CPMP program perform as well as, or better than, graduates of a traditional mathematics curriculum. Graduates of the CPMP program at Andover have, themselves, commented on their preparedness for collegiate mathematics and mathematics-related fields. The following comments are from three students who studied the pilot version of CPMP Course 4. The first two students enrolled at the University of Michigan. Student 1:
In high school, I looked forward to math as one of my favorite subjects. The way I was taught and the instructors who taught it, made Core-Plus math extremely interesting to me. My sophomore year of high school is when I developed such a love for math and science that I decided to go into engineering. In my senior year of high school, I took Calculus BC and placed into Calculus 116 [second semester calculus] here at Michigan. The Core-Plus mathematics system and the calculus class I took [in high school] gave me such a strong base in mathematics that I received an A+ in Calculus 116.
The real-life examples of Core-Plus Mathematics gave me an excellent background for demanding engineering courses. Because of my Core-Plus background, I feel I am two steps ahead of students who did not take Core-Plus math in high school. ... I am able to problem solve much faster than students who do not have a Core-Plus mathematics background. | Student 2:
The first political science class that I took at U of M was Comparative Politics. I was lucky because in Core-Plus Mathematics I learned many different kinds of charts, many different data tables, and many different methods for analysis of data. While many of my peers at college were left wondering what a Pearson's r correlation was, I was asking the professor questions like, "Did you, and by what method, screen out any outliers in the data sets?" I think the biggest advantage of Core-Plus math is that the diversity of topics allows me to feel comfortable in any math setting, whether it is politics, economics, or any subject. | Comments such as the above are not unique to students at the University of Michigan. The following is a quote from an Andover graduate from the same class who enrolled at Stanford University. Student 3:
It is my firm belief that my Core-Plus education in fact better prepared me for the mathematics I encountered in college, as well as for preceding Advanced Placement Examinations, than would have a traditional mathematics program. For any student who intends to study math at the level of single-variable calculus or beyond, I believe that the conceptual-based style of education stressed in the Core-Plus program will prove far more beneficial than the memorization of what would otherwise be meaningless formulas and algorithms. | |
| Q | What are students' perceptions and attitudes about the Core-Plus Mathematics Project curriculum? | | A | A written, Likert-type survey of students' perceptions and attitudes about various aspects of their mathematics course experience was administered at the end of each school year during the field test. In four field-test schools, both CPMP Course 2 students (n = 221) and traditional geometry students (n = 134) completed this survey at the end of their respective courses. (Course 2 results are presented since the newness effect of the CPMP approach is likely to have disappeared by then). Each of the following findings was consistent across levels of pretest student achievement. - Students perceive the CPMP curriculum to be quite difficult, at least as challenging as traditional college-prep mathematics courses. A common perception of students is that CPMP is challenging and makes them think, but they say that with effort they are able to understand the mathematical ideas and their applications.
- Over three-fourths of CPMP and geometry students agreed that cooperative-group work was enjoyable and helped them learn mathematics. The advantages of learning in groups most often cited by students were seeing how other people attack problems and the support of group members during problem-solving efforts.
- A significantly higher percent of CPMP students than of geometry students agreed that their mathematics course made them feel more confident that they could solve mathematical problems (71.1% compared to 55.6%), that they learned to reason mathematically (68.8% to 53.0%), and that the course helped them see that mathematical ideas make sense (64.7% to 51.1%).
- A significantly higher percent of CPMP students than of geometry students agreed that their mathematics course contained realistic problems (76.5% to 47.8%), made the mathematical ideas interesting (70.1% to 41.4%), and increased their ability to talk about (68.2% to 42.9%) and to write about mathematics (66.5% to 40.6%).
- CPMP and geometry students (over 85% of each) agreed that they enjoyed using the calculator in mathematics class. About 70% of both groups also agreed that they learned more mathematics by using the calculator.
- CPMP students were much more likely than geometry students to want to take a mathematics course taught in the same way the next year (75.0% compared to 43.0% agreement), and 27% of CPMP students at the end of Course 3 agreed that it was mainly because of CPMP that they took a third year of mathematics. These findings coupled with substantial increases in enrollments in junior and senior mathematics courses in many field-test schools provide strong evidence that the CPMP curriculum is a factor in keeping more students in mathematics courses longer.
|
Local Implementation
| | Q | What are some tips for effectively implementing the Core-Plus Mathematics Project curriculum? | | A | Based on our experiences working with schools to implement the CPMP curriculum, Contemporary Mathematics in Context, we recommend that careful consideration be given to the form of implementation in a district and to the groundwork needed to build support for school mathematics reform. In addition, a professional development plan to support teachers is crucial to effective implementation of the curriculum. Some things to consider prior to implementation are the following: | | | - As a department, spend time studying the CPMP curriculum and instructional model.
- Build understanding of, and a consensus for, mathematics education reform among administrators, counselors, parents, board members, business/community leaders, other departments within your high school, and middle school faculty.
- Assess district technology needs. A graphing calculator with at least the capabilities of a TI-82/83 is required for each student.
- Develop an extended professional development plan for ongoing support for teachers (see the third question in this section).
- Begin adoption with Course 1 and add a course level each year, allowing teachers to grow with the curriculum.
- Formulate a plan to evaluate your mathematics program and the results of changes made. Plan to collect data over the long term, not just the year or two before and the year or two after the changes.
|
| Q | How can students be accelerated in the Core-Plus Mathematics Project curriculum? | | A | - If your district has a history of enrolling strong eighth-grade students in an algebra course, you may wish to maintain an accelerated program using CPMP Course 1 for select eighth-graders. These students could then enroll in AP Calculus as seniors upon completing Course 4 as juniors. Students can enroll in AP Statistics anytime after completion of Course 3. (Advanced Placement Calculus topics covered in the Core-Plus Mathematics curriculum)
- For students who don't start Course 1 until ninth grade, consider ways to schedule classes to allow students to move through the curriculum more quickly. The following is a list of options that some districts implementing the CPMP curriculum have successfully used.
- A student could double up on classes as a senior by enrolling in both Course 4 and AP Statistics.
- In schools with semester block scheduling, a student could enroll in two courses in a given year.
- In schools with alternate-day academic-year block schedules, the schedule could be adjusted for one or more classes of a course to meet each day for the first semester and classes of the next course similarly scheduled the second semester.
- In schools with traditional academic-year schedules, two mathematics classes may be scheduled back-to-back to allow study of one course in the first semester and the next course the second semester.
- Strong students who have completed one of the NSF-funded middle school mathematics programs, or an algebra course, could enroll in Course 2 in ninth grade. (Some supplemental material on Course 1 topics may be needed.)
|
| Q | What is the role of professional development in implementing the Core-Plus Mathematics Project curriculum? | | A | Because much of the content in statistics, probability, and discrete mathematics is new for many teachers, and because some of the familiar material is developed more fully than in traditional mathematics, teachers need advice and support from other teachers and administrative support in order to implement the curriculum effectively. (Professional Development Opportunities) Active involvement of students also requires a different type of planning by teachers. The Teacher Resource materials encourage teachers to be listening, observing, questioning, facilitating student work, and orchestrating class discussions in new ways. Professional development programs organized around reflecting on practice enable teachers to hone their skills in these areas. At the very least, teachers should attend a professional development workshop led by an experienced CPMP teacher. In addition, schools should strongly consider providing the following supports: - Arrange cooperative learning, technology, and alternative assessment workshops for mathematics teachers before they attend CPMP workshops or begin teaching the curriculum.
- Schedule teaching assignments so that teachers can progress from teaching Course 1 to teaching Course 4 in stages, and thereby develop an understanding of the growth of mathematical ideas across the curriculum.
- Schedule classes to allow for common planning periods for teachers teaching the same course, especially if one or both of them are teaching it for the first time.
|
| Q | What behaviors and characteristics of Core-Plus Mathematics teachers are associated with students' growth in mathematics achievement? | | A | We examined the classroom practices of 20 teachers during the field test of CPMP Course 1. Ten of these teachers comprised the top quartile of field-test teachers and the other 10 the bottom quartile with respect to their students' growth in mathematical achievement over the one-year course. Achievement was measured by a nationally standardized test called the Ability to Do Quantitative Thinking which is the mathematics subtest of the Iowa Tests of Educational Development. The primary data sources were: trained observer's holistic rating of the alignment of the instructional practice and classroom climate with CPMP's teaching for understanding model, self-perceptions of practice by the teachers, and expressed concerns of the teachers about the new curriculum. The research results from this study, summarized below, are reported in a peer-reviewed article published in the Journal for Research in Mathematics Education:
Schoen, H. L., Finn, K. F., Cebulla, K. J., & Fi, C. (2003). Teacher variables that relate to student achievement when using a standards-based curriculum. Journal for Research in Mathematics Education, 34(3) 228-259. The description of the "effective" (i.e., first-quartile) teacher that emerged from analyzing the data from these sources follows. This teacher may be of either gender, but we will use female pronouns for convenience. |
| Q | How does one review and respond to Internet-circulated reports of CPMP that have not been peer-reviewed for publication? The Hill/Parker case | | A | Evaluation studies and research on teaching and learning can contribute in important ways to improving school mathematics. However, research and evaluation reports that have not stood the test of peer review for publication need to be examined carefully. These reports often fail to meet evaluation standards, particularly standards for accuracy. Consider the case of the unpublished report and Thomas Parker entitled, "A study of Core-Plus students attending Michigan State University." This observational study reports trend data on course placement and grades at Michigan State University (MSU) (for years 1996-1999) of students from 6 schools in Michigan that participated in the early pilot- and field-testing of the CPMP curriculum. (For the record, 1999 graduates were the first cohort of students to have the opportunity to study field-test versions of CPMP Courses 1-4.) Separate analyses are provided for 4 schools identified as Core-Plus schools and for 2 schools identified as schools supplementing Core-Plus. A peer review of this report would raise questions about its design, about its methodology, and consequently about any inferences drawn. For example, the authors provide no documentation showing which curriculum units were actually studied by the students. Upon closer examination, in 2 of the 4 schools identified as Core-Plus schools, less than 5% of the 1998 graduating class studied even selected CPMP units. Other schools were identified as supplementing Core-Plus because of offering a precalculus course. But the text used in the precalculus course was, in fact, the CPMP Course 4 text. Thus, the trends described are problematic and, as the authors themselves acknowledge, this report cannot be used to make any causal inferences. Moreover, other data from these same schools indicate that CPMP students perform remarkably well on advanced placement college-level courses - AP Calculus and AP Statistics. These points and others are further discussed below. Design
To be a valid study, the authors need to provide some documentation that the students from each of the 4 schools identified as Core-Plus schools studied the units intended as full preparation for collegiate mathematics. There is no such documentation. Indeed, had the authors carefully studied the context of the schools, they would have prepared a different report. For example, in the case of one district (schools identified as CP4-5) that is singled out for further analysis, only 40 students of the 1998 graduating class of 830 students studied selected CPMP field-test units; and none studied the full program. This represents less than 5% of the graduating class - hardly a Core-Plus class. Most, if not all, of the potential 1998 MSU matriculants from these 2 schools studied traditional college-preparatory mathematics. There is no evidence provided that any of the students with limited exposure to the Core-Plus materials attended MSU in 1998. To underscore the importance of documentation and context analysis, the reader may wish to examine more closely the phased-in implementation of CPMP in schools CP4-5 of the Hill/Parker report. Data from this district show that when fully implemented, CPMP students have a remarkable record of enhanced achievement on examinations judged strong indicators of college preparation - AP Calculus and AP Statistics. Dramatic increases are seen in both the number of students taking these courses and in the number of students scoring 3 or higher on the exams. Hill and Parker identified 2 schools as supplementing Core-Plus because it was believed that these schools offer a traditional precalculus course, and that the teachers in at least one school supplement the Core-Plus program with material intended to develop skill at algebraic manipulation (page 14). There is no further documentation and context analysis of these two schools. Had the authors studied the context of these schools, they would have prepared a quite different report. For example, they would have found that CPMP Course 4 is the text used in the course called "precalculus," because the units covered are precalculus mathematics. Additionally, the authors fail to give any information of how supplementing done by teachers in the supplemented Core-Plus schools is different from supplementing by teachers in the other Core-Plus schools and from supplementing every teacher provides to meet the needs of their students. Data from one of the "supplementing Core-Plus" schools reveals a pattern of implementation and AP achievement similar to that of CP4-5 schools. Methodology
The methodology used by Hill and Parker is not appropriate to the question supposedly being studied. The authors do not provide data on the number of students in each matriculating class at MSU from each of the 4 "pure Core-Plus" schools and what percentage this number is of the total graduates from each of the high schools. Without this information, it is not clear if the same or different proportions of graduates from the schools entered MSU in the years of the study. It is possible that a higher proportion of students chose to attend other universities in the later years of the study. It also may be the case that a higher proportion of graduates attended MSU in 1999, for example, than in 1996 and that these students represent those who would otherwise not go to college, but did so, in part, because of their experiences in the CPMP program. The Hill/Parker report indicates that for CP4-5 (page 12), the number of graduates attending MSU increased from 17 students in 1994 prior to field-testing Core-Plus to 50 students in 2000. The methodology employed makes it impossible to make valid inferences about the cause of observed trends. Course enrollment is confounded with the placement exam used in the Hill/Parker study. If a placement exam only measures algebraic manipulation, then it is possible that students who have more conceptual understanding and problem solving skills may do well in courses beyond what they would be placed in based on a traditional placement test score. This issue of placement tests and the preparedness of CPMP students for collegiate mathematics is carefully examined in a recent paper, "Responding to Calls for Change in High School Mathematics: Implications for Collegiate Mathematics," published in the American Mathematical Monthly, a journal of the Mathematical Association of America. According to the research published in this article, there was no significant difference between CPMP students and students in more traditional programs on the algebra portions of a mathematics placement test at a large midwestern university. On the Calculus-readiness section of the test, the CPMP students scored significantly higher than the traditional students. How well students who have studied a Standards-based curriculum like CPMP perform in college is an important question that needs continued study. Recognizing that placement tests on some campuses remain very traditional, CPMP in the last two years has enhanced its materials to provide better preparation for those types of placement tests. See, for example, the CPMP Reference and Practice books and the 2003 copyright editions of CPMP Courses 1-4, particularly Course 4. Inferences Drawn
Given the conceptual flaws in how the data were collected and what data were included, it is impossible to accurately describe the trends or make causal inferences from this report. This item is also available as a PDF file. |
| Q | A Bachelis-Milgram study is often cited by critics of reform and the Core-Plus Mathematics program. What are the facts about this study? | | A | In 1997, an opinion survey of Core-Plus graduates and non-Core-Plus graduates in a Michigan school district was carried out of Wayne State University. This survey was then analyzed of Stanford University and a report was widely disseminated on the Internet and to the media. This report attempts to conclude that Core-Plus students are not well-prepared for collegiate mathematics. However, the survey is invalid due to serious design flaws and the report draws incorrect conclusions. In spite of this, critics continue to draw attention to the study as a means to create fear of change. Why is the Survey Invalid? Self-reported data: The data are based on self-reported grades and test scores from students. This well-known error in survey research leads to unreliable data. Self-selected sample: The survey is based on a self-selected sample, with no evidence of the makeup of that sample. This well-known error in survey research can lead to biased results. Aggressively biased survey methods: The anti-Core-Plus group funding this survey aggressively campaigned among students. Such activity creates bias in the very group one is trying to survey. Invalid generalizations: The school was using a 1997 pilot curriculum, which no longer exists. As part of the 4-year, data-driven curriculum development process, the curriculum has gone through several years of additional development since 1997. The final version of the Core-Plus curriculum maintains the well-documented strengths of Core-Plus (see frequently asked ), while improving the curriculum in several ways. Incorrect conclusions: This flawed opinion survey attempts to conclude that Core-Plus students are not well prepared for collegiate mathematics. On the contrary, data provided by the University of Michigan registrar indicates that in collegiate mathematics courses at the University of Michigan, graduates of the Core-Plus program perform as well as, or better than, graduates of a traditional mathematics curriculum. Conclusion: Due to fatal research flaws and incorrect conclusions, the Bachelis-Milgram study is not a valid study of the 1997 Core-Plus pilot program at Andover High School. Furthermore, it says nothing about the final Core-Plus curriculum in use today. The invalid claims made on the basis of this single flawed study of one school are in marked contrast to a large and growing body of research that shows the positive effects of the Core-Plus curriculum in a wide range of schools nationally. Results of these rigorous research studies have appeared in refereed journals and presentations at professional conferences. They show the strong positive effects of Core-Plus Mathematics on students' conceptual understanding, problem solving ability, quantitative reasoning, attitudes toward mathematics, and success in advanced mathematical study. For more information about this research, see the Evaluation page, the annotated list of Research Publications, and District Reports from schools using the published version of the Core-Plus Mathematics program.
Schoen, H. L., & Hirsch, C. R. (2003). Responding to calls for change in high school mathematics: Implications for collegiate mathematics. American Mathematical Monthly, February, 109-123.
Schoen, H. L. & Hirsch, C. R. (2003). The Core-Plus Mathematics Project: Perspectives and student achievement. In S. Senk and D. Thompson (Eds.), Standards-Based School Mathematics Curricula: What Are They? What Do Students Learn? pp. 311-344. Hillsdale, NJ: Lawrence Erlbaum Associates, Inc.
Schoen, H. L., Finn, K. F., Cebulla, K. J., & Fi, C. (2003). Teacher variables that relate to student achievement when using a standards-based curriculum. Journal for Research in Mathematics Education, 34(3) 228-259. | |




