Thank you for visiting our site! You landed on this page because you entered a search term similar to this: solving nonhomogeneous second order linear differential equation.We have an extensive database of resources on solving nonhomogeneous second order linear differential equation. Below is one of them. If you need further help, please take a look at our software "Algebrator", a software program that can solve any algebra problem you enter!
MM - 455 DifferentialEquations
Free Undamped Motion of Spring/Masssystem
Recall from Calculus I, Hooke's Law for springs, F= kx, where F is the force, k is the spring constant and x is thedisplacement beyond equilibrium. Then we found the work done instretching or compressing the spring by integrating the force overthis distance. What we are to do now is find the equation of motionof the spring after it is stretched or compressed and then released.For free undamped motion where there is no resistance from thesurroundings, the differential equation 
,where k is the spring constant, and m the mass( use slugs, notpounds, in the Engish system ) of the object at the end of thespring, is solved for x[ t ] the displacement of the springat any time t. In these problems, displacement belowequilibrium is positive. Also, the constant
,is used.
For example, if a spring has k = 8, m = 2, x( 0 )= 4, x'( 0 ) = 6, the differential equation to be solved is x''( t )+ 4x( t ) = 0, x( 0 ) = 4, x'( 0 ) = 6. Here the mass m is 2 slugswhich means the weight is 64 pounds. The x( 0 ) = 4 is the positionof the weight at t = 0 which is 4 units below equilibrium length. Theinitial velocity x'( 0 ) = 6 means that the spring was given a pushdownward at 6 ft/sec. The solution obtained from DSolve[{x''[ t ] + 4x[ t ] == 0, x[ 0 ] == 4, x'[0 ] == 6 }, x[ t ], t] is x[ t ] = 4 Cos[2t ] + 3 Sin[ 2t ]. Its graph is:
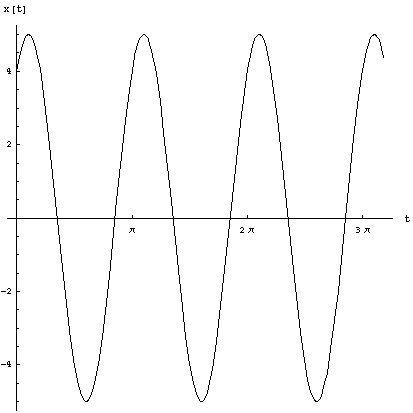
The above graph plots the motion of thedisplacement of the spring with respect to equilibrium over time. Theactual motion of a spring of length 10 ft, with an equation of motionx( t ) = 10 + 2sin( 2t ) - 6cos( 2t ) is:
Free Damped Motion
When the surroundings offer resistance to thespring, damped motion results. It is clear from the above solutionthat undamped is unrealistic as the motion of the spring will notlast forever. For damped motion, a damping constant,
,is the constant proportional to the velocity of the spring. Theresulting second order linear equation is:
,where 
.There are three possibilities here:
In the overdamped or critically damped cases, thespring moves through equilibrium at most one time. In an underdampedsituation the spring moves through equilibrium two or moretimes.
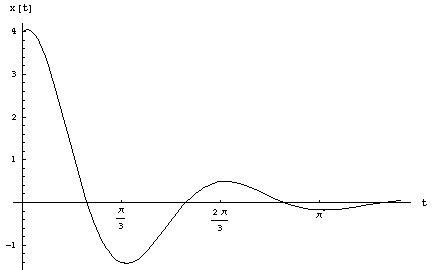
For example, if m = 1, k = 10, = 2, x'( 0 ) = 2, x( 0 ) = 4, the differential equation is: x''( t )+ 2x'( t ) + 10x( t ) = 0 and is underdamped. The solution is x( t )= e( -t )( 4cos( 3t ) + 2sin( 3t ) ) with thegraph:
Driven Motion
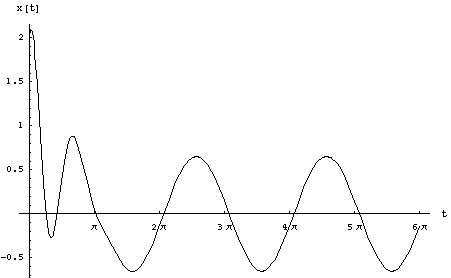
If the spring is attached to an external force, f(t ), the differential equation becomes nonhomogeneous. Now we mustsolve:
.Let's apply a force of f( t ) = 6sin( t ) to the above system andsolve. The solution is
.It is agood thing that Mathematica is doing all the work! Please notethat the first part will go to 0 as t increases. This part is thetransient part while the second part is the steady state. Here is thegraph:
LRC Circuits
The spring/mass systems are analagous to LRCcircuits, where the transient and steady state terms are derived. Thedifferential equation to be solved is 
,where the constants are precisely what we have alreadydone.
Things to know and do
- Set up, solve and graph a spring/mass system.
- Given a force of 32 lbs. moves a spring 1 ft. beyond equilibrium and a damping constant numerically equal to 2 times the instantaneous velocity, graph the equation of motion if the initial position is 4 ft beyond equilibrium and the initial velocity is 2 ft/sec downward. Graph the resulting motion if a force of sin( t ) + 2cos( t ) is driving the system.