Thank you for visiting our site! You landed on this page because you entered a search term similar to this: solving quadratic equations by completing the square.We have an extensive database of resources on solving quadratic equations by completing the square. Below is one of them. If you need further help, please take a look at our software "Algebrator", a software program that can solve any algebra problem you enter!
| 2x + 7x = 4 | |
| 2x + 7x – 4 = 0 | To get the equation in standard form, subtract 4 from each side; one side must be 0 when solving by factoring |
| (2x – 1)(x + 4) = 0 | Factor left side of equation |
| 2x – 1 = 0 or x + 4 = 0 | Set each factor equal to 0, using the Zero Factor Property |
| 2x = 1 x = -4 x = | Solve each of the resulting two equations |
The solution set is 
Solving Quadratic Equations Using the Square Root Property
A quadratic equation of the form x
= kcan be solved using the following property:
Square Root Property: The solution set of x
= kis 
Example. Solve: a) 4x
= 20
b) z
= -49
Solution. a)
4x = 20 | |
 | Divide both sides by 4 to isolate x |
 | Simplify |
x = ±  | Use the square root property to obtain two solutions |
The solution set is 
b)
| z= -49 | |
z =  | Use the square root property |
| z = ± 7i | Simplify the radical |
The solution set is 
Solving Quadratic Equations by Completing the Square
To solve a quadratic equation by completing the square, theequation must be written in the form (x + n)
= k.The following steps are used to solve the equation
ax+ bx + c = 0 , a ¹0 , by completing the square:
1. If a ¹ 1, divide both sidesof the equation by a.
2. Rewrite the equation so that the constant term is isolatedon one side of the equation.
3. Take half the coefficient of x and square this result; addthis square to both sides of the
equation.
4. Factor the resulting trinomial as a perfect square; combinelike terms on the other
side.
5. Use the square root property to complete the solution.
Example. Solve by completing the square: 2x + 5x– 4 = 0.
Solution.
2x + 5x – 4 = 0 | |
 | Divide both sides by 2 |
 | Add 2 to both sides to isolate the constant |
Take half the coefficient of x and square it: 
 | Add  to both sides of the equation |
 | Factor the trinomial; add the constants |
 | Use the square root property |
 | Add - to both sides and simplify the radical |
The solution set is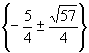 
Solving Quadratic Equations Using the Quadratic Formula
The solutions of the quadratic equation ax+ bx+ c = 0 , a ¹ 0, are
The following steps are used to solve a quadratic equationusing the quadratic formula:
1. Write the equation in standard form, ax
+ bx+ c = 0.
2. Determine the values of a, b, and c; a is the coefficientof x
, b is the coefficient of x,
and c is the constant.
3. Substitute these values of a, b, and c into the quadraticformula.
4. Simplify.
Example. Solve using the quadratic formula: 3x
= 2x– 4
Solution.
| 3x = 2x – 4 | |
3x - 2x + 4 = 0 | Write the equation in standard form. |
| a = 3, b = -2, c = 4 | Determine the values of a, b, and c |
| | The quadratic formula |
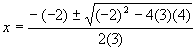 | Substitute the values of a, b, and c into the formula |
 | Simplify |
 | |
 | |
 |