Problema Solution
A random sample of 100 students attending a concert spent an average of $142 on their tickets with a standard deviation of $47.50.
Calculate the 90%, 95%, and 99% confidence intervals for the mean amount of money spent by all students attending the concert.
Answer provided by our tutors
The formula for a confidence interval for a population mean is:
![]()
deviation, n is the sample size, and z* represents the appropriate z*-value from the standard normal distribution for your desired confidence level.
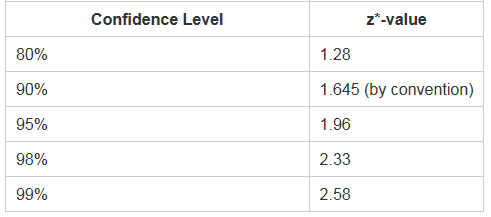
90% confidence intervals for the mean amount of money spent by all students attending the concert is:
142 + 1.645*(47.50/√100) = 149.81
142 - 1.645*(47.50/√100) = 134.19
The confidence interval is (134.19, 149.81).
95% confidence intervals for the mean amount of money spent by all students attending the concert is:
142 + 1.96*(47.50/√100) = 151.31
142 - 1.96*(47.50/√100) = 132.69
The confidence interval is (132.69, 151.31).
99% confidence intervals for the mean amount of money spent by all students attending the concert is:
142 + 2.58*(47.50/√100) = 154.26
142 - 2.58*(47.50/√100) = 129.75
The confidence interval is (129.75, 154.26).