Problema Solution
A rectangular piece of metal is 30 in longer than is wide squares with sides 6 in long are cut from the four corners and the flaps are folded upward to form an open box if the volume of the box is 2706 in cubed what were the original dimensions of the piece of metal
Answer provided by our tutors
Let
x = the wide of the rectangular piece, x>0
x + 30 = the length of the rectangular piece
h = 6 in is the height of the open box
V = 2706 in^3 is the volume of the open box
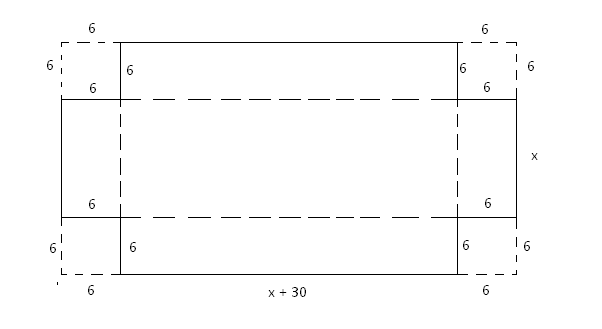
Since the volume of open box is equal to the product of the area of the base and the height we have:
V = (x - 2*h)(x + 30 - 2*h)*h
V = (x - 2*6)(x + 30 - 2*6)*6
Thus we have the following quadratic equation:
(x - 2*6)(x + 30 - 2*6)*6 = 2706
........
click here to see the equation solved for x
........
x = 23 in
23 + 30 = 23 + 30 = 53 in
The original dimensions of the rectangular piece of metal are: the length is 53 in and the width is 23 in.