Problema Solution
An animal feed to be mixed from soybean meal and oats must contain at least 120
lb of protein, 18
lb of fat, and 10
lb of mineral ash. Each sack of soybeans costs $ 15
and contains 50
lb of protein, 6
lb of fat, and 5
lb of mineral ash. Each sack of oats costs $5
and contains 15
lb of protein, 5
lb of fat, and 1 lb of mineral ash. How many sacks of each should be used to satisfy the minimum requirements at minimum cost?
Answer provided by our tutors
Let
x = sacks of soybean meal
y = sacks of oats
We have the following limitations:
50x + 15y >= 120
6x + 5y >= 18
5x + 1*y >= 10
x >= 0
y >= 0
The objective function (the cost) is:
F(x, y) = 15x + 5y
The function F(x, y) = 15x + 5y has minimum in one of the corner points of the graph:
50x + 15y >= 120
6x + 5y >= 18
5x + 1*y >= 10
x >= 0
y >= 0
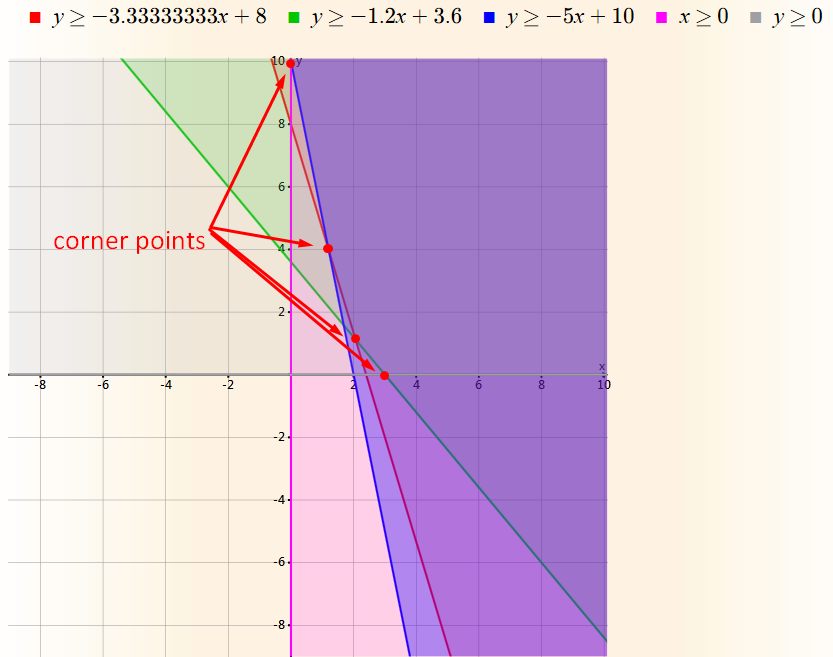
The corner points are: (3, 0), (0, 10), (33/16, 9/8) and (6/5, 4)
F(3, 0) = 15*3 + 5*0 = $45
F(0, 10) = 15*0 + 5*10 = $50
F(33/16, 9/8) = 15*(33/16) + 5*(9/8) = $36.5625
F(6/5, 4) = 15*(6/5) + 5*4 = $38
The minimum cost is achieved for 33/16 = 2.0625 sacks of soybean meal and 9/8 = 1.125 sacks of oats.