Problema Solution
A rancher has 600 feet of fencing to put around a rectangular field then subdivide the field into 3 identical smaller plots by placing two fences parallel to one of the field’s shorter sides. Find the dimensions that maximize the enclosed area.
Answer provided by our tutors
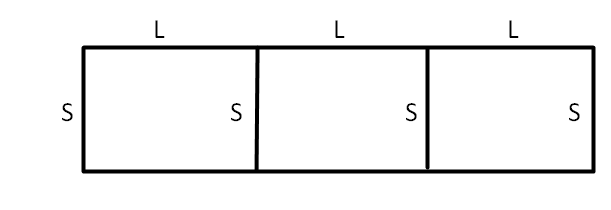
First, let's write an equation for the amount of fencing needed for the end result (3 identical co-joined fields) where 'L' stands for the long side and 'S' stands for the short side.
Fencing
Fencing =4S+6L
4S+6L = 600
6L = 600 - 4S divide both sides by 2
3L = 300 - 2S
The enclosed area is:
A = S*(3L)
A = 3SL
To maximize the enclosed area, we need to make 'A' dependent on only one variable. Then we can take the derivative of 'A' with respect to that variable and set the derivative equal to 0 to find the max point.
A= S*3L
A = S(300 - 2S)
A = -2S^2 + 300S
A' = -4S + 300
Set the deravitive to 0 and solve for 'S':
-4S + 300 = 0
S = 300/4
S = 75 ft
Now we can find L:
3L = 300 - 2S
L = (300 - 2S)/3
Plug S = 75
L = (300 - 2*75)/3
L = 150/3
L = 50 ft
The dimensions that maximize the enclosed area are 50 ft by 75 ft.