Addition and Subtraction of Rational Numbers
Example 3 Add or subtract the fractions, as
indicated. Use primes to find the least common
denominator. Be sure to simplify all answers.
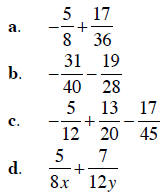
Solution a. Start by finding the prime
factorizations of 8 and 36:
8 = 2 • 4 = 2 • 2 • 2
36 = 4 • 9 = 2 • 2 • 3 • 3
The LCM must have three 2’s and two 3’s, which is:
LCM = 2 • 2 • 2 • 3 • 3 = 72
Now build the fractions to the LCM , combine numerators , and simplify:
 |
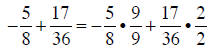converting to common denominators |
 |
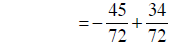building fractions |
 |
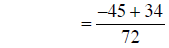combining fractions |
 |
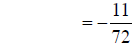adding numerators |
b. Start by finding the prime factorizations of 40 and 28:
40 = 4 •10 = 2 • 2 • 2 • 5
28 = 4 • 7 = 2 • 2 • 7
The LCM must have three 2’s, one 5, and one 7, which is:
LCM = 2 • 2 • 2 • 5 • 7 = 280
Now build the fractions to the LCM, combine numerators, and simplify:
 |
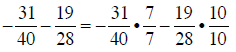converting to common denominators |
 |
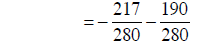building fractions |
 |
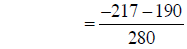combining fractions |
 |
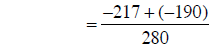changing to addition |
 |
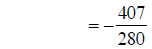adding numerators |
c. Start by finding the prime factorizations of 12, 20, and 45:
12 = 4 • 3 = 2 • 2 • 3
20 = 4 • 5 = 2 • 2 • 5
45 = 9 • 5 = 3 • 3 • 5
The LCM must have two 2’s, two 3’s, and one 5, which is:
LCM = 2 • 2 • 3 • 3 • 5 = 180
Now build the fractions to the LCM, combine numerators, and simplify:
 |
|
 |
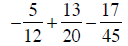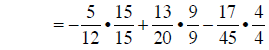converting to common denominators |
 |
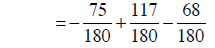building fractions |
 |
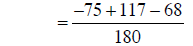combining fractions |
 |
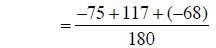changing to addition |
 |
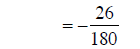adding numerators |
 |
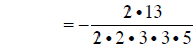cancelling common factors |
 |
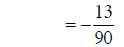multiplying factors |
d. Start by finding the prime factorizations of 8x and
12y:
8x = 2 • 2 • 2 • x
12y = 2 • 2 • 3 • y
The LCM must have three 2’s, one 3, one x, and one y, which is:
LCM = 2 • 2 • 2 • 3 • x • y = 24xy
Now build the fractions to the LCM and combine numerators:
 |
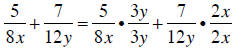converting to common denominators |
 |
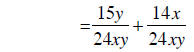building fractions |
 |
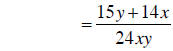combining fractions |
Notice how we cannot do any further simplification of this
resulting
fraction. In algebra you will learn some techniques which can be applied to
simplify fractions such as this one.
When dealing with mixed numbers, two different approaches
can be used. If we are adding two
mixed numbers, both of which are positive, the easiest approach is to add the
whole number and
fraction portions separately. For example, to add
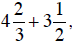we first add the two fractions :
 |
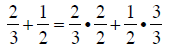converting to common denominators |
 |
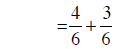building fractions |
 |
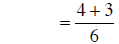combining fractions |
 |
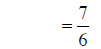adding fractions |
 |
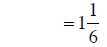converting to mixed number |
Now adding the mixed numbers:
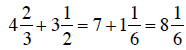
However, when negative numbers become involved, this method becomes rather
tricky. Thus, to
compute the subtraction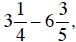 
it is best to
convert the mixed numbers to fractions and
compute directly:
 |
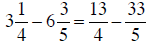converting to fractions |
 |
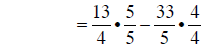converting to common denominators |
 |
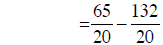building fractions |
 |
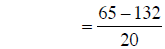combining fractions |
 |
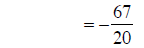subtracting fractions |
 |
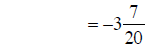converting to mixed number |
Unless we are adding positive mixed numbers, it is this
second approach we will use to combine
mixed numbers.
Example 4 Combine the mixed numbers, as indicated.
Be sure to simplify any answers and
convert answers to mixed numbers.
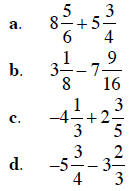
Solution a. Since we are adding positive mixed numbers, we
can use the first approach.
Start by adding the two fractions:
 |
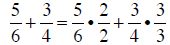converting to common denominators |
 |
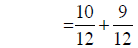building fractions |
 |
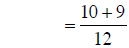combining fractions |
 |
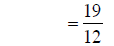adding fractions |
 |
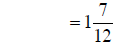converting to mixed number |
Now adding the mixed numbers:
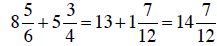
b. Converting the mixed numbers to fractions, then combining:
 |
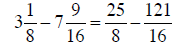converting to fractions |
 |
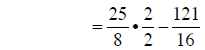converting to common denominators |
 |
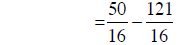building fractions |
 |
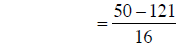combining fractions |
 |
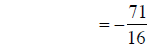subtracting fractions |
 |
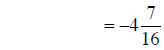converting to mixed number |
c. Converting the mixed numbers to fractions, then combining:
 |
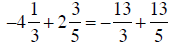converting to fractions |
 |
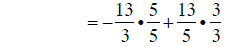converting to common denominators |
 |
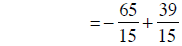building fractions |
 |
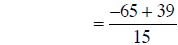combining fractions |
 |
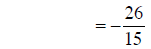adding fractions |
 |
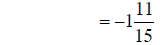converting to mixed number |
d. Converting the mixed numbers to fractions, then combining:
 |
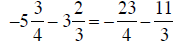converting to fractions |
 |
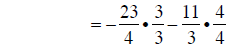converting to common denominators |
 |
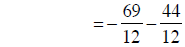building fractions |
 |
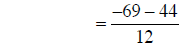combining fractions |
 |
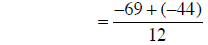converting to addition |
 |
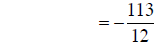adding fractions |
 |
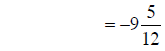converting to mixed number |
Whereas adding and subtracting fractions and mixed numbers
involves a number of steps in
finding the common denominator, the same operations for decimals are fairly easy
to apply.
Since the decimal system involves tenths, hundredths, thousandths, etc, the
place-values used
already represent common denominators. Thus, to compute 15.89 + 7.643, we only
need to be
sure the decimal points are lined up so that the place- values are also lined up.
Usually we insert
place-value holders (0), line up the decimal points, then just add as with whole
numbers. The
sum is therefore:
11 1
15.890
+7.643
23.533
Subtraction is performed similarly, except that borrowing (rather than carrying)
is involved.
Example 5 Perform the following additions and
subtractions.
a. 45.982 + 6.57
b. 9.9 + 23.864
c 5.07 - 3.295
d. 6.4 - 9.86
Solution a. Lining up the decimal and inserting
place-value holders:
111
45.982
+6.570
52.552
b. Lining up the decimal and inserting place-value holders:
11
9.900
+23.864
33.764
176
c. Lining up the decimal and inserting place-value holders:
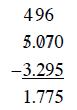
d. This is actually trickier than it looks. Since 9.86 is larger than 6.4, this
subtraction will result in a negative number. To find out how much it will be
negative, we actually need to reverse the subtraction:
9.86
-6.40
3.46
Since the value is actually negative, 6.4 - 9.86 = -3.46 .
Terminology
least common denominator
Exercise Set 3.3
Add or subtract the fractions, as indicated. Be sure to
simplify all answers.
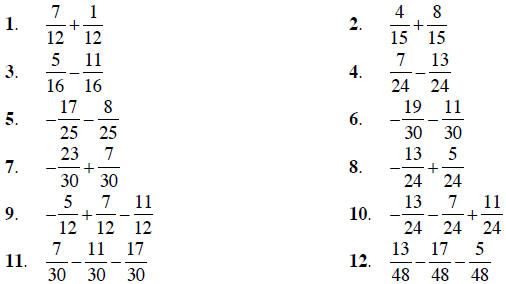
Add or subtract the fractions, as indicated. Be sure to
simplify all answers.
Add or subtract the fractions, as indicated. Use primes to
find the least common denominator.
Be sure to simplify all answers.
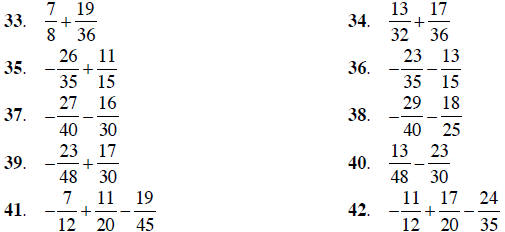
Combine the mixed numbers, as indicated. Be sure to simplify any answers and
convert answers
to mixed numbers.
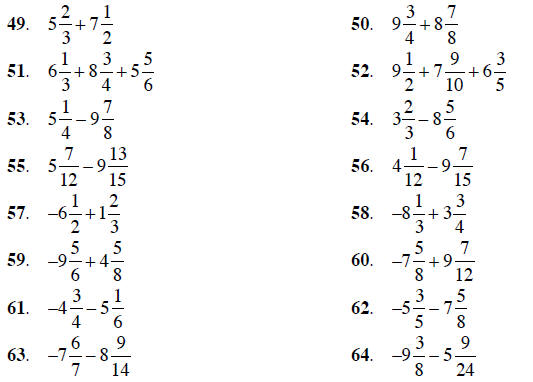
Perform the following additions and subtractions.
65. 18.95 + 9.473
66. 23.876 + 8.49
67. 6.99 + 25.808
68. 7.98 + 24.376
69. 14.07 - 9.683
70. 103.62 + 56.954
71. 25 - 14.46
72.
32 - 16.85
73. 102 - 28.407
74. 115 - 65.749
75. 8.3 - 12.473
76. 6.7 - 14.826
77. 5.2 - 13.104
78. 4.7 - 26.43
79. -8.5 - 25.77
80. -14.56 - 29.859
Answer each of the following application questions. Be
sure to read the question, interpret the
problem mathematically , solve the problem, then answer the question. You should
answer the
question in the form of a sentence.
81. Maurice has $458.62 in his checking account, and
writes checks for $15.87, $132.45,
and $88.60. What is his new balance in the account?
82. Sylvia has $682.36 in her checking account, and writes checks for $45.86,
$102.39,
$23.69, and $16.70. What is her new balance in the account?
83. After writing a check for $78.97, Carolyn has $196.87 in her checking
account. How
much was in her account before writing the check?
84. After writing a check for $199.68, Mary has $679.54 in her checking account.
How
much was in her account before writing the check?
85. After depositing a check for $795.84 in his checking account, Alfred has
$1669.86 in
his savings account. How much was in his account before depositing the check?
86. After depositing two checks for $186.52 and $337.50 in her account, Norma
has
$1156.40 in her savings account. How much was in her account before depositing
the
checks?
87. John buys a stock at a price of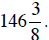 
During
the next day it rises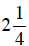 
, then it drops
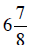the following day. What is the price of the stock after these two days?
88. Dennis buys a stock at a price of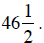 
During the next day it drops 
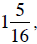then it rises
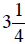the following day. What is the price of the stock after these two days?
89. Three pieces of lumber are stacked on top of each other. The first piece is
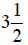inches
thick, the next piece is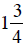 
inches thick, and the third piece is 
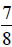inches thick. How
thick is the stack of three pieces of lumber?
90. Three pieces of lumber are stacked on top of each other. The first piece is
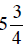inches
thick, the next 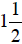piece is 
inches
thick, and the third piece is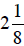 
inches thick. How
thick is the stack of three pieces of lumber?
| Prev | Next |