Algebra and Geometry Strands-The
Algebra and Geometry Strands-The Standards for Algebra I
Where Do We Meet?
Introduction:
This lesson covers objectives in the algebra and geometry strands of the New
York State
standards for Algebra I. The students will use the graphs of systems of linear
equations to
find the solution for the systems . The students will work in cooperative groups
to graph
linear equations and find the point of intersection. This is a lesson to be used
prior to
teaching substitution and elimination for solving systems of linear equations.
One day of 40
minute instruction is needed for this lesson.
New York State Standards:
Mathematics, Science, and Technology - Standard 3
Students will:
•understand the concepts of and become proficient with the skills of
mathematics ;
•communicate and reason mathematically;
•become problem solvers by using appropriate tools and strategies;
through the integrated study of number sense and operations , algebra,
geometry, measurement, and statistics and probability.
Algebra Strand
Students will represent and analyze algebraically a wide variety of problem
solving
situations.
A.A.40 Determine whether a given point is in the solution set of a system of
linear
inequalities .
Geometry Strand
Students will use visualization and spatial reasoning to analyze characteristics
and
properties of geometric shapes.
A.G.7 Graph and solve systems of linear equations and inequalities with rational
coefficients in two variables .
Objectives
1. The students will be able to graph two linear equations on the same graph.
2. The students will be able to find the solution for a system of linear
equations by
finding the intersection on a graph.
3. The students will be able to check their solution in the given system of
equations.
Instructional Protocol
This is an introductory lesson to solving systems of equations. It is expected
that students
already have experience graphing lines and know how to name the coordinates of a
point .
There is a cooperative learning portion of the lesson along with a section of
direct
instruction. Included is a worksheet that students will work on during guided
instruction
along with extra problems for the students to work on inside and/or outside of
class.
Materials:
Graph Paper
Rulers
Index Cards
Yarn or Tape (to marker a path on the floor)
Overhead Projector/ Transparencies
Guided Notes
Lesson:
1. Hook: Ask for four volunteers to help with the following activity.
• Start with two students standing in each of two corners of the room. (Not
two opposite corners).
• In each of the two corners, one student will hold the end of the yarn on the
floor.
• The other two students will take the yarn and walk from their corner to the
opposite corner and put the yarn on the floor, pulling it tight.
• Explain to the students that the yarn on the floor represents the path the
students walked.
• Go to where the yarn intersects and ask the students what this location
means. (The one place that both students walked through. Where they
would run into each other if they are there at the same time.)
• Explain that two linear equations is called a system of equations, and the
solution is where they intersect.
2. Put students into groups of three or four for the cooperative learning
activity. Each
task is written on an index card to hand out at the appropriate times to each
group .
The groups will also need a piece of graph.
• Task 1 (5 min.): Graph the line y = 3x + 5.
• Task 2 (5 min.): Graph the line 12x + 3y = -6 .
• Task 3 (5 min.): Find the coordinates of the intersection of the two graphs
and check this point in both equations. (Solution: (-1,2))
3. Go over the solution on the overhead projector by bringing up volunteers to
show
what they did for each task. Explain that the solution is not only where the two
lines meet but the point where the two equations are equal.
4. Ask the students what the solution is for a system of linear equations where
the
lines are parallel. (Answer: There is none since the lines never intersect.)
5. Ask the students if a system of linear equations can have two solutions.
(Answer:
No, two lines intersect at no more than one point.)
6. Give the students the “Graphing Systems of Linear Equations” Worksheet and go
over solving the first system. If there is time students may continue working on
the
worksheet in groups or individually and the rest of the worksheet can be the
homework assignment.
Extension Activity:
Have students think about whether they can use this method for solving systems
of
equations that are not lines. Also, students can think about reasons why
graphing may not
be the best method for solving systems of equations.
Graphing Systems of Linear Equations
1. Solve the following system of linear equations by graphing.
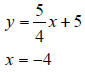
2. Solve the following system of linear equations by graphing.
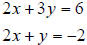
3. Solve the following system of linear equations by graphing.
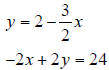
| Prev | Next |