Math Practice Test
____ 1. For the following function, first find all values of x such that
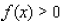then find all x such that
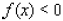
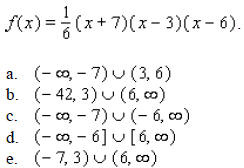
____ 2. If one zero of the following function is 4, find the other two zeros.
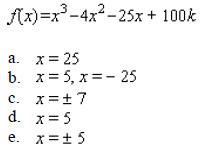
____ 3. Use the remainder theorem to find
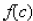
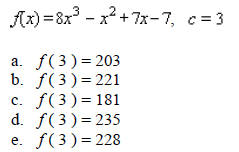
____ 4. Use the factor theorem to decide whether x-c is a factor of the polynomial.
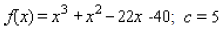
a. x - c is a factor
b .x - c is not a factor
____ 5. Use synthetic division to decide whether c is a zero of
.
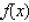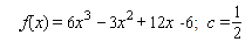
a. x - c is a zero
b. x - c is not a zero
____ 6. Find a polynomial with leading coefficient of 1, degree 3, and zeros: -5,0,9.
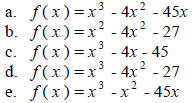
____ 7. Use synthetic division to find the quotient and remainder if the first polynomial is divided by the second.
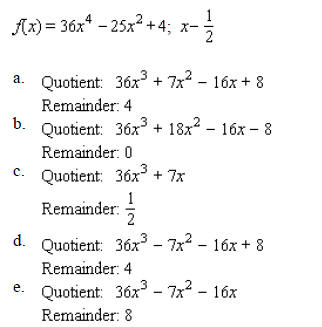
____ 8. Find a polynomial
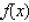of degree that has the indicated zeros and satisfies the given condition.
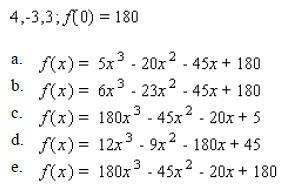
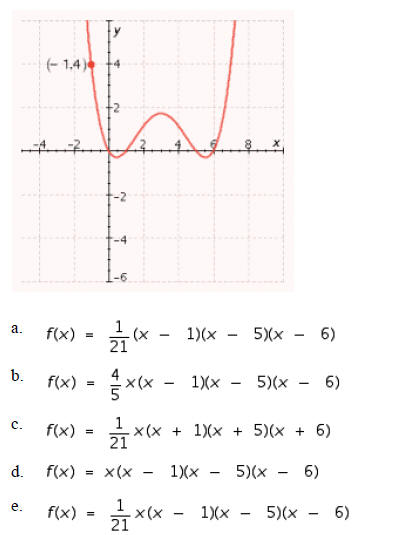
____ 9. Find the fourth-degree polynomial function whose graph is shown in the figure.
____ 10. A polynomial f ( x ) with real coefficients and leading coefficient 1 has the given zeros and degree. Express f ( x ) as a product of linear and quadratic polynomials with real coefficients that are irreducible over R.
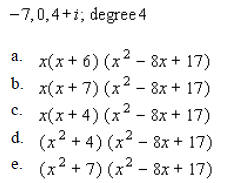
____ 11. Find the oblique asymptote of
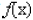
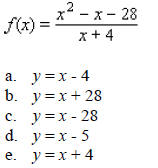
____ 12. Determine whether the function f is one-to-one
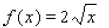
a. one-to-one
b. not one-to-one
____ 13. Use the theorem on inverse functions to determine whether f and g are inverse functions of each other.
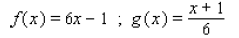
a. f and g are inverse functions of each other.
b. f and g are not inverse functions of each other.
____ 14. Determine the range of
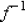for the function without actually finding
.
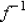Hint: First find the domain and range of f
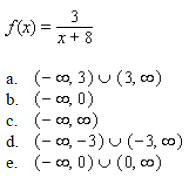
____ 15. Find the inverse function of f
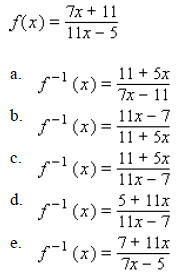
____ 16. Solve the equation :
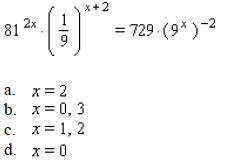
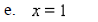
____ 17. Sketch the graph of f if:
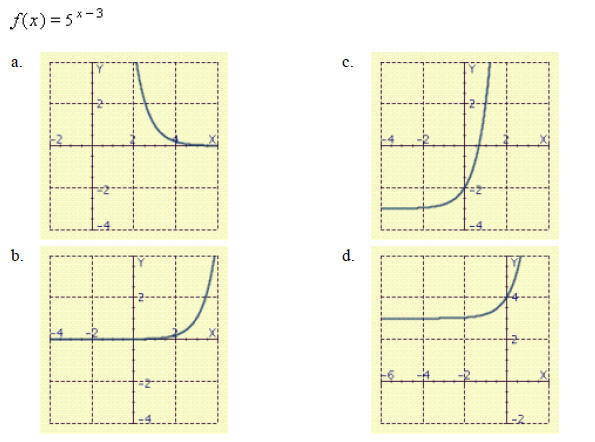
____ 18. Find an exponential function of the form f (x) = bax that has the given y-intercept and passes through the point P:
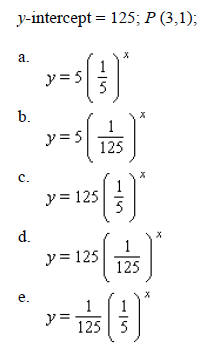
____ 19. The number of bacteria in a certain culture increased from 600 to 1,800 between 7:00 A.M. and 9:00 A.M. Assuming the growth is exponential, the number f (t) of bacteria t hours after 7:00 A.M. is given by:
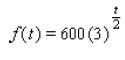
Estimate the number of bacteria in the culture at 10:00 A.M.
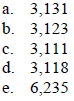
____ 20. The radioactive bismuth isotope 210Bi has a half-life of 5 days. If there is 100 milligrams of 210Bi present at t = 0, then the amount f(t) remaining after t days is given by:
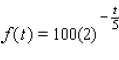
How much 210Bi remains after 25 days?
a.8.125 milligrams
b.12.125 milligrams
c.2.125 milligrams
d.3.125 milligrams
e.5.125 milligrams
____ 21. In 1980, the population of blue whales in the southern hemisphere was thought to number 5,000. The population N(t) has been decreasing according to the formula
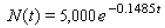
where t is in years and t = 0 corresponds to 1980. Predict the population in the year 2010 if this trend continues.
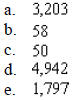
____ 22. Use the graph of y = ex to help sketch the graph of
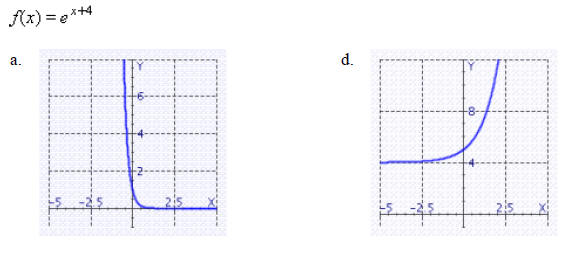
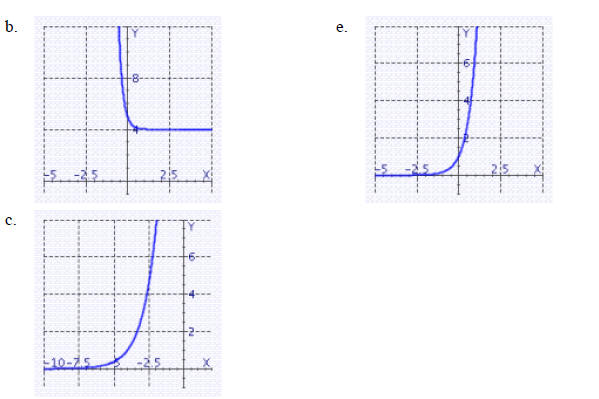
____ 23. If $900 is deposited in a savings account that
pays interest at a rate of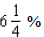 
per year
compounded continuously , find the balance after 7 years.
a.$1,369.77
b.$581.08
c.$1,393.95
d.$1,418.56
e.$3,484.87
____ 24. An investment of $835 increased to $16,771 in 20 years. If the interest was compounded continuously, find the interest rate.
a.14%
b.30%
c.17%
d.15%
e.12%
____ 25. The 1980 population of the United States was approximately 227 million, and the population has been growing continuously at a rate of 0.7% per year. Predict the population in the year 2040 if this growth trend continues.
a.322 million people
b.229 million people
c.345 million people
d.382 million people
e.379 million people
____ 26. Change to exponential form.
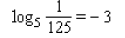
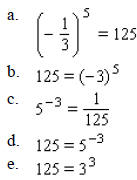
____ 27. Solve the equation.
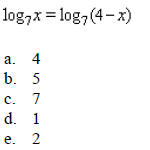
____ 28. Solve the equation.
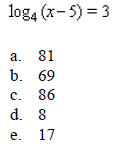
____ 29. Express in terms of logarithms of x , y, z, or w.
____ 30. Write the expression as one logarithm.
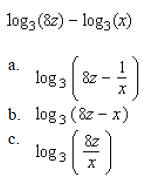
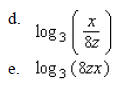
____ 31. Solve the equation.
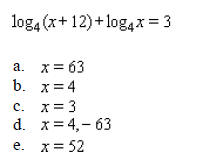
____ 32. Find the exact solution, using common logarithms, and an approximation of the solution of the equation to two decimal places .
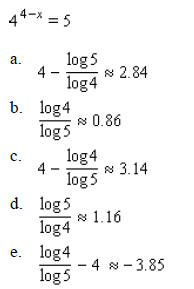
____ 33. Use the compound interest formula to determine how long it will take for a sum of money to double if it is invested at a rate of 6% per year compounded monthly.
a.11.58 years
b.16.67 years
c.11.90 years
d.14.75 years
e.10.41 years
Multiple Response
Identify one or more choices that best complete the statement or answer the
question.
____ 34. Find the zeros of
, and state the multiplicity of each zero.
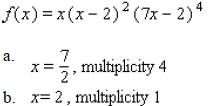
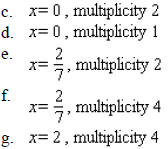
____ 35. Use Descartes' rule of signs to determine the number of possible positive, negative, and nonreal complex solutions of the equation.
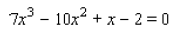
a.0 positive roots , 3 negative roots, 0 nonreal roots
b.2 positive roots, 1 negative root , 0 nonreal roots
c.1 positive root, 0 negative roots, 2 nonreal roots
d.1 positive root, 2 negative roots, 0 nonreal roots
e.3 positive roots, 0 negative roots, 0 nonreal roots
f.0 positive roots, 0 negative roots, 3 nonreal roots
practicetest2_ch3_4
Answer Section
MULTIPLE CHOICE
1. ANS:E
2. ANS:E
3. ANS:B
4. ANS:A
5. ANS: A
6. ANS:A
7. ANS:B
8. ANS:A
9. ANS: E
10. ANS: B
11. ANS: D
12. ANS:A
13. ANS:A
14. ANS: E
15. ANS: C
16. ANS: E
17. ANS: B
18. ANS: C
19. ANS: D
20. ANS: D
21. ANS: B
22. ANS: C
23. ANS: C
24. ANS: D
25. ANS: C
26. ANS: C
27. ANS: E
28. ANS: B
29. ANS: A
30. ANS: C
31. ANS: B
32. ANS: A
33. ANS: A
MULTIPLE RESPONSE
34. ANS: B, D, F
35. ANS: C, E
| Prev | Next |