Zeros of a function
As we continue graphing various functions it becomes more
and more important to
discover the zeros, or the roots. We move away from calling these numbers x axis
intercepts because sometime the values that make f(x) = 0 are complex numbers
and can’t
be graphed…so we call any x that makes the calculated value = 0 a zero or a root
of the
function .
For f(x) = x2 + 49
Let’s look at f (x) = x2 +49
Use CTS to find the roots. Graph the function. See why we
call them zeros or roots
rather than x intercepts?
What are the x intercepts?
Note that complex numbers always come in pairs – a complex
number and its complex
conjugate.
If 3i is a root, then -3i is, too - ALWAYS pairs if complex!
a + bi and a - bi will always be together as roots, or zeros.
You can use synthetic division to check for roots and
thereby get some polynomial
factored. If the remainder is zero, then the value you used as a divisor is a
root and the
factor is x + the additive inverse of the root or zero.
An example: f (x) = x3 +16x
Domain
End behavior,
y intercept
x intercepts
roots
An example:
Is 5 a zero of f (x) = x2 -10x + 25 ? Check using synthetic division:
Yes, it is a zero - one that is also an x axis intercept.
The associated factor is (x - 5) and it has multiplicity 2.
Note: Is 5 a zero? and Divide by (x - 5) are the SAME instructions!
Is -3 a zero of x2 + 7x -10 ?
Check using synthetic division.
Note that you get a graph point from synthetic division
when you’re doing it on a
polynomial with points. Related to but slightly different from the use of
synthetic
division last lecture.
Now the question quickly becomes – how do you know which
numbers to check and
which numbers to ignore? There’s a handy theorem, called the
Rational Root Theorem
that takes care of all the guessing:
Take all the factors of the constant term (aka the constant coefficient)
Successively divide each of those by the factors of the
coefficient of the leading term…
this will produce a list of all the possible rational roots or zeros…if none of
these works
out then you have to try complex or irrational roots.
Mnemonic: R = C/L (alphabetical order on the right )
Let’s make a list of all the possible rational roots of f (x) = 2x2 +11x +12
These are the only numbers you need to try to find the
zeros of the parabola. In this case,
complete the square might be quicker…and old fashioned factoring is quickest of
all.
Let’s look at one where you have no alternatives like CTS
to help you.
We’ll work it all the way out:
f (x) = 2x4 -x3 -8x2 + x +6
ok – even positive leading coefficient – end points in
same direction and up
(0, 6) is the y intercept…
zeros?
Possible zeros:
Try with x = 2
Factors with multiplicities:
Graph:
Let’s try another one: f(x) = x3 - x2 + 4x - 4
Domain
End point behavior and y intercept
Possible zeros:
Try with x = 1
Now you have to use CTS on the sum of two squares :
Factors and multiplicities:
So graph the function:
positive leading coefficient, odd – opposite ends…left down, right up
y intercept is -4
zeros are:
Suppose I told you I wanted to build a function:
degree is 3; zeros of -1, 1, 2; constant coefficient of 6
What will the formula be and what will the graph look like?
Now let’s build one with degree 6; zeros of 2i, -1
(multiplicity 2), i and a constant
coefficient of 16.
And one with degree 2 and a zero of -2i.
Review problem:
Use long division to find the remainder:
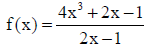
Use synthetic division to find the quotient and remainder
of
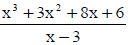
| Prev | Next |