Numbers and interval notation
We first look at sets of numbers and conclude with
notation for certain kinds of sets of real numbers.
Let Z, Q, and R denote the sets of integers, rational numbers , and real numbers,
respectively.
Let N denote the set of natural numbers. Let C denote the set of complex numbers
(also known as
the complex plane).
When every element of a set A is also an element of another set B, we say that A
is a subset
of B and express this relationship in symbols as A
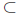B. With this subset notation we can express
the relationship between the various sets of numbers compactly as
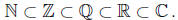
(1) The set N of natural numbers consists of the whole, or counting, numbers {1,
2, 3, . . . , n, . . .}.
(2) We get the next larger set Z of ( positive and negative ) integers from the
set of natural numbers
N by adding to N the solutions of all equations like x + b = a, where a and b
are natural
numbers. We can denote the solution x using subtraction as x = a - b. For example,
x+3 = 5
yields nothing new, namely x = 5 - 3 = 2, but x + 5 = 3 does, namely x = 3- 5 =
-2.
(3) The set Q of rational numbers is obtained by adding to the set of integers Z
the solutions of
all equations like b x = a where b is not zero. For example, 3 x = 12 gives
nothing new as
x = 12/3 = 4, but 3 x = 11 does, namely x = 11/3.
(4) The set of real numbers R is larger still. Every rational number can be
expressed in decimal
form. For example, 3/8 = 0.375 or 1/3 = 0.333 333 . . . . That not all
quantities were rational
numbers (ratios of whole numbers) was known to the Pythagorean Greeks two
millennia
ago. Indeed there is a very simple proof , attributed to Euclid, that the square
root of two is
irrational. In symbols, this means that the equation x2 = 2 has no solution in
the set Q of
rational numbers. In a certain sense, almost all decimal numbers are not
rational, but to see
this requires a fair amount of effort. For example, F. Lindemann, in 1882, was
the first person
to show that π = 3.141 592 65 . . . was not only not rational, but was not the
solution of any
polynomial equation with integer coefficients.
(5) The set C of complex numbers is obtained from the set R of reals numbers by
adding all
the solutions to all polynomial equations with real coefficients. For example,
although the
equation x2 + 2 = 3 gives us nothing new, namely x2 = 3-2 = 1, so x = ±1, the
equation
x2 + 3 = 2 does. Indeed, in this case x2 = -1 and we can denote the two (complex
or
imaginary) solutions as
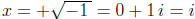and
.
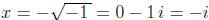However, we have now reached the end of our journey. Considering polynomial
equations with
complex coefficients we have reached closure: no new numbers are required.
Although much anticipated,
both Leonhard Euler (1707.1783) and Nicolaus Bernoulli (1687.1759) realized that
every
n-th degree polynomial equation with complex coefficients had n complex roots , a
fully rigorous
demonstration of the Fundamental Theorem of Algebra had to wait for Carl
Friedrich Gauss' 1799
proof.
Interval notation is a compact way to identify
uninterrupted portions of the set of real numbers.
We consider the set of real numbers that are not negative and that are not
bigger than one.
(1) The set I of real numbers from zero to one , including both zero and one.
(2) The set I is the set of numbers x that are real and such that zero is less
than, or equal to, x
and x is less than, or equal to, one.
(3) I = {x ∈ R| 0 ≤ x and x ≤ 1}.
(4) The set I = [0, 1 ].
More generally, we have the following two conventions for bounded intervals.
(a, b) = {x ∈ R|a < x < b} is the open interval from a to b.
[ a, b] = {x ∈ R| a ≤ x ≤ b} is the closed interval from a to b.
There are four kinds of unbounded intervals:
(a,∞) = {x ∈ R|a < x}
[ a,∞) = {x ∈ R| a ≤ x}
(−∞, b) = {x ∈ R|x < b}
(−∞, b] = {x ∈ R| x ≤ b}
In the preceding , the (finite) number a is the left endpoint and the number b is
the right endpoint.
Note than in the case that a = b, the open interval (a, a) = (b, b) has no
elements, i.e., is empty.
The empty set is denoted by Ø. On the other hand [ a, a ] just consists of the
one number a. Not
much of an interval, right?
Question: What numbers belong to the set [ 0, 10)?
| Prev | Next |