Math 281 Exam 1
Read the problems. Read them again. Make sure to express your answers
in a clear and logical way. Don't rush!
1. (20 pts.)
Prove the following identity:
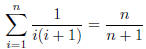
(5 pts. extra credit if you find a proof not by induction)
Hints and pointers:
(a) You can do a standard proof by induction here. Remember, a proof
by induction always consists of two steps . First, you need to assess
the validity of your formula for some basic case (e.g. n = 1). Second,
you assume the formula true for a generic n and from this you deduce
the validity of the formula for n + 1. Note that this often involves
manipulating parts of the formula for n + 1 so that you can reduce
it to the formula for n and some simple stuff .
(b) This identity lends itself also to a proof that does not involve
induction,
but for that a clever idea is required: find some A and B such
that
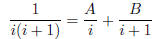
then start experimenting with this summation!
2. (20 pts.)
Prove that the set of real numbers which are roots of some quadratic
polynomial with integer coefficients is a countable set. In other words:
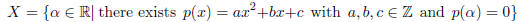
You must prove X is a countable set.
(5 pts. extra credit if you find two different proofs )
Hints and pointers:
Here there are two possible ways to prove this fact. The following questions
should lead you on the right track:
(a) How many quadratic polynomials with integer coefficients are there
(e.g. countably many or uncountably many?) For each polynomial,
how many roots can it have?
(b) How do you write down the roots of a quadratic equation ? (Quadratic
formula).
The two questions lead you in different directions, both of which work.
You certainly will want to make use of the theorems that we stated in
class:
•a countable union of countable sets is countable,
•a finite cartesian product of countable sets is countable,
•a countable union of finite sets is countable.
3. (20 pts.) Describe a bijection between an open disc in the plane and the
whole plane. In other words, let
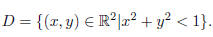
You need to describe a function:
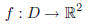
and show f is a bijective function.
Hints and pointers:
First o , you need to really understand what you are trying to do here!
You need to give me a function that associates to any point in the open
disc a point in the plane. This function must be into and onto!
This exercise is very similar to a problem in project 3. Note that there
you defined a bijection between (-1, 1) and all of R.
Also remember that you can, if you want, use polar coordinates on the
plane .
4. (25 pts.) If X is a finite set, prove that a function
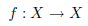
is injective if and only if it is surjective. Show that this needs not be
true
if X is an infinite set.
Use this fact to prove that if p is prime every non-[0] element in Z/pZ has
a multiplicative inverse .
Hints and pointers:
First o , if you have two finite sets, and an injective function between
them, can you say something about which set has "more" elements? How
about if you have a surjective function?
The second part is trickier, and it requires being familiar with
multiplications
in Z/pZ. First try experimenting with multiplication tables for
various Z/pZ. Try to see what elements m have multiplicative inverses,
and if you can relate this to properties of m and n .
Then think of the function mult[n] : Z/pZ -> Z/pZ. What does it mean
for n to have a multiplicative inverse in terms of this function ? But then
if you want to prove that mult[n] is ****, maybe you can instead use the
previous part of the exercise to show that mult[n] is ***.
5. (20 pts.)
Show that if z1 and z2 are two (complex) roots of 1 such that z2-z1 = 1,
then they are 6-th roots of 1. In symbols :
if
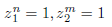
and
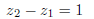
then
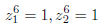
Caution: be very careful about what you are
actually proving. I am not
asking you to prove that there exist two sixth roots of unity with that
property.
Hint: you might want to think about the geometric
representation of
roots of 1 (where do all roots of 1 live?). Also, take a complex number z.
Plot it on the plane. Then plot z-1. Where is z-1 with respect to z?
| Prev | Next |