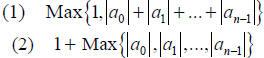Zeros of a Polynomial Function

L19 Zeros of a Polynomial Function

Division Algorithm for Polynomials

If f and g are two polynomials and g is not the
zero polynomial, then there are the unique
polynomials q (quotient) and r (remainder) such
that

where r(x) either the zero polynomial or of degree
less than the degree of g(x).

Note: If g(x) = x − c, then f (x) = q(x)(x − c) + r ,
where r is a number.

If x = c, then f (c) =

Remainder Theorem

If a polynomial f (x) is divided by (x − c), then the
remainder r = f (c).

Example: Find the remainder if f (x) = x⁴ − 6x³ + 2 is
divided by (x + 2). Use
synthetic division

the Remainder Theorem

Example: Use the Remainder Theorem to find f (3) if
f (x) = x⁶ − 6x⁵ + 54x² −16x +1

Note: If the polynomial f (x) is divided by (x − c) and
the remainder r = 0, then f (c) = 0, that is, c is a
zero of f (x).

Example: If f (x) = x³ − 6x + 4, is 2 a zero of f ?

Factor Theorem

The polynomial (x − c) is a factor of the polynomial
f (x) if and only if f (c) = 0.

Proof:
If (x − c) is a factor of f , then f (x) =
hence f (c) =

If f (c) = 0, then r = f (c) = and f (x) =
therefore (x − c) is a factor of f .

Example: Is (x −1) a factor of x³ − 2x +1?

Example: Factor f (x) into linear factors given that c is a
zero of f (x).

f (x) = 3x³ − 5x² −16x +12;
c = −2

Fundamental Theorem of Algebra

Every polynomial of degree 1 or more has at least
one complex zero .

Let deg f (x) = n, n ≥1
Zeros:

Number of Zeros Theorem

A polynomial of degree n has at most n distinct zeros.

Note: A polynomial of degree n has exactly n complex
zeros if to count each zero as many times as its
multiplicity .

Conjugate Zeros Theorem

If f (x) is a polynomial whose coefficients are real ,
and if a + bi is a zero of f (x), with a and b real
numbers, then a − bi is also a zero of f (x).

Example: One zero is given, find all others

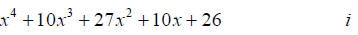
Example: Find the polynomial of degree 3 with real
coefficients that satisfies the conditions:

zeros @ −2,1, 0

f (−1) = −1

Example: Find a polynomial of the lowest degree
possible with only real coefficients which has the given
zeros:

−1
6 − 3i

Bounds of Zeros

Let M > 0.
A number M is called a bound on zeros of a polynomial f
if everyreal zero c lies between – M and M, inclusive,
that is,

−M ≤ c ≤ M

Theorem: Let f denote a polynomial of degree n whose
leading coefficient is 1.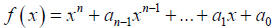

A bound M on the real zeros of f is the smallest of the
two numbers:

Notes: 1) If the leading coefficient of the polynomial
f (x) is not 1, that is, a_n≠1 , in order to use the Theorem
you can replace f (x) with the polynomial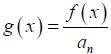
since f ( x) has the same zeros as g(x).

2) The bounds on the zeros give a good choice of
Xmin and Xmax of the viewing rectangle since all the x- intercepts
of the graph can be seen .

Example: (a) Find bounds on the real zeros of the
polynomial function f ( x) = −3x³ + 8x² − 6x + 9.

(b) Use a graphing utility to graph the polynomial in the
viewing rectangle determined by the bounds on the zeros.
Approximate the real zeros (x-intercepts).

Intermediate Value Theorem

If f (x) is a polynomial with only real coefficients
and if for real numbers a and b, the values f (a) and
f (b) are of opposite signs , then there exists at least
one real zero between a and b.

Example: Show that the polynomial has a real zero
between 2 and 3.
f (x) = 2x³ − 9x² + x + 20