Quadratic equations
Quadratic equations have a rich history, having intrigued
mathematicians
and engineers from antiquity. The first known solution of a quadratic equation
hails
from Egypt—recorded in the Berlin papyrus from the Middle Kingdom (ca. 2160-1700
BC). In essence, the two equation non- linear system to be solved was:
x2 + y2 = 100 and y = ¾ x
Solutions providing only the positive root were proffered by Indian, Persian,
and
Greek mathematicians over a period that spanned from 500 BC to 1100 AD, 1600
years! Most of these solutions were geometric ones.
This document serves as a tutorial on quadratic equations. After completing this
tutorial, you should be able to:
I Solve quadratic equations by
1. factoring.
2. the square root method.
3. completing the square.
4. using the quadratic formula.
II Find the discriminant of a quadratic equation and use
it to determine
how many solutions and the type of solutions the equation possesses.
One method may be more thorough, the other more efficient, depending on
the quadratic equation given. So it is good to be versatile in the various
approaches to solve quadratic equations. The frequent utility of quadratic
equations in the physical sciences mandates our familiarity with the essential
algebraic manipulations. So, here we go,……
Quadratic Equation—Standard form: ax2 + bx + c = 0 ; a ≠ 0.
Now, a linear equation is cast in the form ax + b = 0 ; the highest power of x
is 1. Similarly, for a quadratic equation, the highest power of x is 2. There
are four ways to solve quadratics, that is, to determine the zeroes of the
equation :
| 1 | Solving Quadratic Equations by
Factoring—a quadratic equation may be solved by factoring if , after writing it in standard form, the quadratic expression factors . |
|
| Step 1: | Simplify each side . This would
involve things like removing ( ), removing fractions , adding like terms , etc. To remove fractions: Since fractions are another way to write division, and the inverse of divide is to multiply, you remove fractions by multiplying both sides by the LCD of all of your fractions . |
|
| Step 2: | Write in standard form, if needed—squared
term is written first left term linear in x is second and the constant is third—equation set equal to zero. |
|
| Step 3: | Factor. | |
| Step 4: | Use the Zero-Product Principle. If
ab = 0, then a = 0 or b = 0. The only way a product can become 0 is if at least one of its factors is 0. That is why it is important to cast quadratic equation in standard form. |
|
| Step 5: | Solve for the linear equation(s)
set up in Step 4. If a quadratic equation factors, it will factor into either two identical linear factors or two distinct linear factors. Thus the equations found in step iv will be linear equations. |
|
| Example 1: | Solve by factoring. 25x2 - 40x = -16 Let’s apply the 5 steps in turn: | |
| Step 1: | Simplify each side if needed. | |
| Add 16 to both sides: | ||
| Step 2: | Write in standard form, if needed. | |
| Step 3: | Factor. 25x2 -40x +
16 = A2x2 +(2AB)x + B2 if the two
factors are identical or [ACx2 +(AD+ B C) x + BD] which is the expansion of form (Ax + B) (Cx + D) if the two factors are different . Assume integers. Now it’s a matter of trial and error: |
|
| Step 4: | Use the Zero-Product Principle | twice. |
| Step 5: | Solve for the linear equation(s) set up in step 4. | |
| Example 2: | Solve by factoring. | |
| Step 1: | Simplify each side if needed. | |
| Add -5x to both sides: | ||
| Step 2: | Write in standard form, if needed. | |
| Step 3: | Factor.. 12 = 3 · 4 or 6 · 2.
Try A = 6 and C = 2, what must B and D be? Inspecting (6x + B) (2x + D) = 12x2 + 5x - 2 = 0 BD must equal -2. |
|
| Thus try A = 3 and C = 4 Again term BD must equal -2. Now: | ||
| Step 4: | Use the Zero-Product Principle | |
| either (3x + 2 ) OR (4x -1 ) vanishes. | ||
| Step 5: | Solve for the linear equation(s) set up in step 4. | |
| There are two solutions to this quadratic equation: | ||
| Example 3: | Solve by factoring x(2 + 15x) = -1 | |
| Step 1: | Simplify each side. | |
| Distribute left hand side: | ||
| Move all terms to right side: 2x + 15x2 = -1 | ||
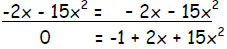 |
||
| Step 2: | Write in standard form, if needed. | |
| Step 3: | Factor. 15 = 3 · 5 Try A = 5
and C = 3, what must B and D be? Inspecting (5x + B) (3x + D) = 15x2 + 2x - 1 = 0 product BD must equal -1. |
|
| Step 4: | Use the Zero-Product Principle | |
| Step 5: | Solve for the linear equation(s) set up in step 4. | |
| There are two solutions to this
quadratic equation: (2) Solving Quadratic Equations by the Square Root Method--You can solve a quadratic equation by the square root method if you can write it in the form . |
||
| Step 1: | Write the quadratic equation in the form if needed. | |
| F and G represent algebraic
expressions. When the quadratic equation appears in this form, solution by the square root method is best. |
||
| Step 2: | Apply the square root method. | |
If F and G are algebraic
expressions such that F2 = G, then , 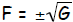 also written F = ±G½ In other words, if you have an expression squared set equal to another expression, the inverse operation to solve it is to take the square root of both sides. Since both a positive and its opposite squared result in the same answer, then you will have two answers, plus or minus the square root of G. |
||
| Step 3: | Solve for the linear equation(s) set up in step 2. | |
| After applying the square root method
to a quadratic equation you will end up with either one or two linear equations to solve |
||
| Example 4: | Solve 5x2 = 2.45 by using the square root method. | |
| Step 1: | Write the quadratic equation in the form if needed | |
| Step 2 and 3 : | Apply the square root method and solve: | |
| Example 5: | Solve by using the square root method. (x – 2)2 = 16 | |
| Step 1: | Write the quadratic equation in the form if needed –already done | |
| Step 2: | Apply the square root method. | |
| Step 3: | Solve for the linear equation(s) set up in step 2. | |
| Example 6: | Solve 3 = (1 – 2x)2by using the square root method. | |
| Step 1: | Write the quadratic equation in the form if needed | |
| AND Step 2: | Apply the square root method. | |
| Step 3: | Solve for the linear equation(s) set up in step 2. | |
 |
Add 2x and subtract
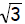 from both sides: from both sides: |
|
The other solution is: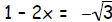 |
Add 2x and
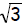 from both sides from both sides |
|
| Thus, the solutions are : written more compactly as : |
||
| Example 7: | Solve -3 = (1 – 4x)2 by using the square root method. | |
| Step 1: | Write the quadratic equation in the form if needed | |
| AND Step 2: | Apply the square root method. | |
Note that the square root of
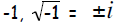 where i is the imaginary where i is the imaginarynumber . Thus, the square root of 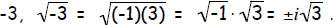 |
||
| Step 3: | Solve for the linear equation(s) set up in step 2. | |
| Thus, the solutions are: written more compactly as : 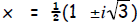 |
||
| Prev | Next |