Applications of Quadratic Formula
Use the Quadratic Formula to solve the following giving
approximate answers to the nearest thousandth
unless otherwise instructed.
1. The base of a triangle is 4 cm. longer than the height. The area is 45 sq.
cm. Find the base
and height.
2. The length of a rectangular plot of land is 132 ft. longer than the width. If
the area is 96133
ft2 find the length and width. Hint: the answers are integers with product
96113.
3. One leg of a right triangle is 9 cm. longer than the other. The hypotenuse is
50 cm. Find the
length of the legs to the nearest mm.
4. The late Manas Torcom, a rug dealer in Park Ridge, wanted to make a rug in
the shape of a
regular octogon (8 sided figure, all sides the same length) from a square 2
yards (72 inches)
to a side by cutting isosceles triangles off of each corner of the square . What
should the
dimensions of each triangle be and what is the length of each side of the
resulting octogon?
Give answers as mixed numbers to nearest 1/8 inch.
5. Dave and Dick, working together, tile a large floor in 30 hours. If they
worked alone it
would take Dick 5 hours longer than Dave to do the job. How long would it take
each
working alone? Hint: if it takes Dave t hours and Dick r hours then the formula
would be
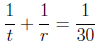
6. An object is thrown upwards from the roof of a
building. The the height above the ground in
meters at time t is given by the equation
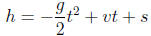
where v is the initial upwards velocity in meters per
second, s is the height in meters
above ground level of the release point and g is the acceleration of gravity
which averages
9.8 m/sec2 on earth but varies slightly from location to location, and t is time
in seconds
from the release time.
Given that in this particular instance g = 9.78m/sec2, v = 8.24m/sec and s =
15.72m
find how many seconds after release will the object hit the ground? Give answer
to nearest
hundredth of a second.
7. In addition to itself , the number 1 has two complex cube roots . Find them.
Hint: You need
to solve x 3 = 1 for all solutions. But note the factorization x3 − 1 = (x −
1)(x2 + x + 1)
so these complex cube roots satisfy the quadratic equation x2 + x + 1 = 0. Give
exact and
approximate answers, to 4 decimal places , for these cube roots. Check!
8. The golden mean is an important irrational ( not a fraction ) number in
mathematics . This
positive number g has the property that g 2 = g + 1. Give exact and approximate
values, to 7
decimal places , for g.
| Prev | Next |