APPLICATIONS OF SOLVING EXPONENTIAL EQUATIONS USING LOGARITHMS
APPLICATIONS OF SOLVING EXPONENTIAL EQUATIONS USING LOGARITHMS
1) Depreciation (the decline in cash value ) on a car can be determined by the
formula V = C(1− r)t , where:
V = the value of the car after t years
C = the original cost
r = the rate of depreciation
If the car's cost, when new, is $15,000, the rate of depreciation is 30%, and
the
value of the car now is $3,000, how old is the car to the nearest tenth of a
year?
2) Growth of a certain strain of bacteria is modeled by the equation G =
A(2.7)0.584t
where:
G = final number of bacteria
A = initial number of bacteria
t = time (in hours)
In approximately how many hours will 4 bacteria first
increase to 2,500 bacteria?
Round your answer to the nearest hour.
3) The amount A, in milligrams, of a 10-milligram dose of
a drug remaining in the
body after t hours is given the formula A =10(0.8)t . Find, to the
nearest tenth of
an hour, how long it takes for half of the drug dose to be left in the body.
4) Sean invests $10,000 at an annual rate of 5% compounded
continuously ,
according to the formula A = Pert , where:
| A = amount | r = rate of interest |
| P = principal | t = time (in years) |
| e = 2.718 |
a) Determine, to the nearest dollar, the amount of money
he will have after 2 years.
b) Determine how many years, to the nearest year, it will take for his initial
investment to double.
5) The equation for radioactive decay is
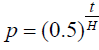 where:
where:
p = the part of the substance
H = half-life of substance
t = period of time that the substance remains radioactive
A given substance has a half-life of 6,000 years. After t
years, one-fifth of the
original sample remains radioactive. Find t, to the nearest thousand years.
| Prev | Next |