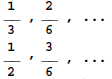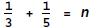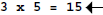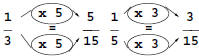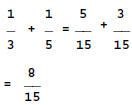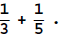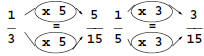Comparison of 5th grade textbooks
As the author’s math-ignorant daughter and a full-fledged
graduate of the
California education system is applying to PhD programs in comparative lit-
erature, her revengeful parent is compiling these notes in the aforementioned
genre.
The subjects for the comparison are Singapore and California, 5th grade
textbooks:
Primary Mathematics 5A, US Edition, Federal Publications, Ministry of
Education, Singapore , and
Mathematics, book 5, California Edition, Houghton Mifflin Company.
Figures 1 and 2 reproduce page 37 from Singapore and page 332 from California
respectively, representing the same topic chosen almost randomly.
In Figure 1, a boy from Singapore tells us a short story requiring the addition
of 1/3 and 1/2. The square prompts invite us to feed in the answer 5/6. This
was not hard, but the question remains: how did the boy guess to replace the
fractions with respectively 2/6 and 3/6? Is there a secret, a trick? Is he a
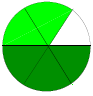
genius? No, the boy explains, it was a stroke of luck: as the picture shows,
the cake was precut into 6 equal parts, of which Ann took 2 and her brother 3.
Now the general idea is revealed: the problem of adding 1/3 and 1/2 looked
hard because the denominators were different, but using equivalent fractions
with the same denominator makes the problem easy.
In the next two pages, a girl and the boy will help us examine equivalent
fractions in 3 more addition and 3 subtraction examples with common de-
nominators climbing up to 30. These will be followed by 3 addition and 3
subtraction exercises to be solved on our own , and respectively — by two
pointers to homework sets from Workbook 5A. A page of Practice with 12
more exercises and several word problems will conclude unit 2. Addition and
Subtraction of Unlike Fractions .
 Addition and Subtraction of Unlike Fractions Ann ate 1/3 of a cake. Her brother ate 1/2 of the same cake. What fraction of the cake did they eat altogether?
They ate
They are called unlike fractions.
They are called like fractions .
|
Figure 1
We note the precise and economical character of the text: not a sign is
wasted.
On the contrary, the multicolor Figure 2 from California
asks for an editor’s
red pen.

Add Fractions With You will learn how to add fractions which have
Learn About It Most of Earth’s surface is covered by water.
|
|||||||||||||
Figure 2
The opening promise “You will learn how to add fractions which have dif-
ferent denominators” only reiterates the title (or does it? — we will come to
this later) and can be safely omitted. The satellite picture of the Earth is of
no use and better be dropped too. The scientifically true fact that “Most of
Earth’s surface is covered by water” does not really follow from 8/15 > 1/2
and, being presently irrelevant, should be removed as well .
“Find 1/3+1/5” is a perfect mathematical formalization of the problem and
stays. A cyborg’s thought process “Add. 1/3 + 1/5 = n” reads “a third and
a fifth add up to n” and goes, since it refers to an n which has not been
introduced (nor is going to show up later).
My limited English does not allow me to “Notice that the fractions are
different unit lengths”. Fortunately the entire Step 1 is redundant : drawing
the fractions on the number line does not facilitate the addition.
“Use the product of the denominators to write equivalent fractions with a
common denominator” explains the plan perfectly and leaves no reason to
repeat it in Step 2. Likewise, the instruction “Rewrite the problem using
fractions. Then add” in Step 3 adds nothing new after “Find 1/3+1/5”.
Removing it also helps one to realize that there is no need to chop the solution
into “steps”.
The result of our editing, shown in Figure 3, matches Figure 1 in clarity and
simplicity. Yet something still displeases the ear, doesn’t it? Who the heck
are these unlike denominators?
In Singapore (and most of the world), unlike fractions have different denom-
inators. Respectively, like fractions have equal denominators and are in this
sense similar, or “friendly” (as some teachers put it), “speaking the same lan-
guage” of sixths or fifteenths. Like fractions are not necessarily equal, so the
word comes handy. Embarrassingly, in California, the scholarly term unlike
denominators stands simply for different ones, so that like means nothing but
the same.
One can deepen the comparison by noting the variance in the methods of
addition of fractions in Singapore and California: the mental scan of equiva-
lent fractions until they become ”friendly” often yields smaller denominators
than the product routine. In fact the next Lesson in California introduces
Least Common Denominators and uses prime factorization, while the Singapore
math program postpones studying prime factorization until grade 7. One
may debate if this makes California ultimately more advanced, or argue that
in practice the method in Singapore is just as efficient, or probe educational
advantages of either approach.
One may further discuss how wise it is to fake scientific applications and
pretend doing algebra, or try to guess the consequences of replacing ideas with
algorithmic ”steps”. One may wonder what role is left to thinking when the
command think is used as an euphemism for do, or why Singapore students
don’t get a separate subtraction unit while California students need it.
 Add Fractions With Unlike Denominators The Pacific Ocean
covers about 1/3 of Earth’s Find Use the product of the denominators to write
|
Figure 3
All these subtleties are entirely beside the point, which is: California is
poorly written, period. The book is on the list of instructional materials
adopted by the California Department of Education in 2001 and features links
to California Math Standards pagewise, yet it is grossly redundant, full of
irrelevant details, misleading explanations, confusing comments, distracting
pictures, embarrassing mistakes.
Dear fellow mathematicians,
On those rare occasions when you are given the role of Content Reviewer of
a school textbook, please — may it even be the last sum of cash you receive
for such services — let common sense be your guide and the red pen your
weapon!
I need your courage and sacrifice: my son has just entered the California
education system.
| Prev | Next |
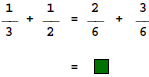

 of the
cake altogether.
of the
cake altogether.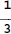 and
and
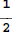 do not have the same denominator.
do not have the same denominator.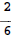 and
and
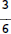 have the same denominator.
have the same denominator.