Real Analysis I: Hints for Problems of Chapter 3
Section 3.3
1.
 |
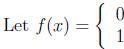if x is rational |
| if x is irrational |
Let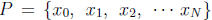 
be any partition
of [0, 1]. Then in any subinterval 
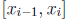, we can
pick a
rational number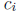 
and an irrational number
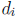so that
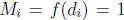and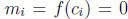 
.
Thus for any
partition P, we have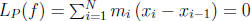 
, while
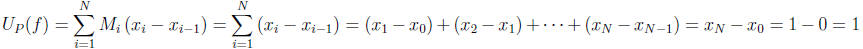
. f is not Riemann integrable sinc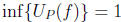e 
while
.
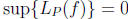2. Let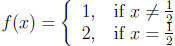
Let ε > 0 be given. Let 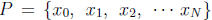be any partition of
[0, 1] such that the length of the largest
sub interval is less than ε. (It is a matter of choosing N so large that ε >
1/N.) Suppose 1/2 is in the jth
subinterval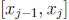 
. On this subinterval
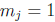while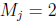 
.
On all other subintervals we have 
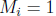and
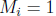(why?). We now have
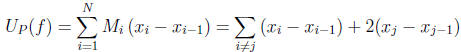
and
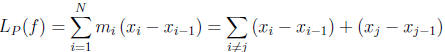
Subtracting the two equations we get
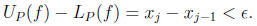
Therefore, f is Riemann integrable by Lemma 3 (Page 89).
3. Suppose f is Riemann Integrable and f(x) ≥ 0 for all x ∈ [a, b]. (a) To show
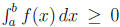, let
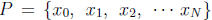. Then for each subinterval
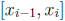of this partition, we have
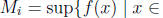
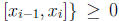. (Explain why
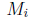should be ≥ 0.) But then
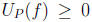and hence 
.
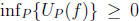By
definition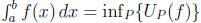 
and hence
.
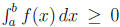(b) Suppose f(x) ≥ 0, f is continuous and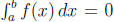 
.
We need to show f(x) = 0 for all x. Suppose
not. Then there exists a number c in [a, b] such that f(c) > 0. Since f is
continuous, there exists a delta > 0
such that f(x) > 0 for all x in [a, b] and |x − c| ≤
.
We can choose smaller,
if necessary, so that c −
and
c + are in [a, b]. Let
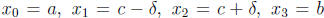. Then 
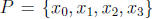is
a partition of
[a, b].( Draw a number line and show this partition.) Since f(x) ≥ 0 on the
first and the third subintervals
we have, 
and
. On the second subinterval
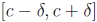, the function is continuous. Hence it
attains its maximum and minimum. On this interval (by the choice of)
f(x) > 0 for all x. In particular
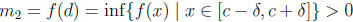. Thus
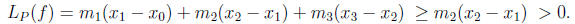
Since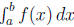 
is greater than or equal to any lower
sum we see that
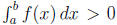. This contradicts the
assumption.
(Note: Once we assume that f(c) > 0 for some c, and f(x) ≥ 0 for all x, then
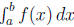is the area of a region
under the graph and hence it must be positive. This is what we proved above, a
seemingly trivial statement!!)
4. Let f(x) = 3x on [0, 1]. and let ε > be given.
(a) Let = ε/3. Then
for all x and for c in [0, 1], |x − c| ≤
implies |f(x) − f(c)|≤
. Now choose a
positive integer N large enough so that 1/N <
and let
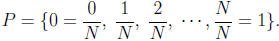
For each subinterval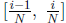
, we have
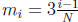and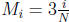 
.
( Draw the graph of f(x) = 3x and use N = 8
to see this or simply observe that the function is increasing.) But then
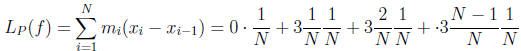
and
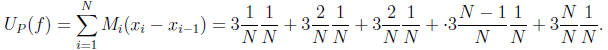
Hence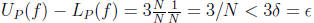 
as required.
(b) Let k be any integer and let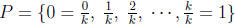 
. Let
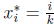. Then 
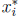is in the subinterval
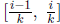. Note then that
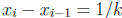and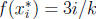 
. We
form the Riemann sum
.
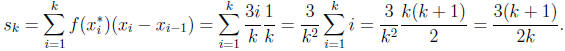
Thus by Corollary 3.3.2 (page 91), we have
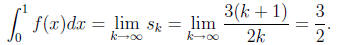
5. Since f is continuous on [a, b], by Corollary
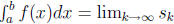, where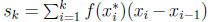 
is a Riemann sum. Any Riemann sum can be divided into parts where f is positive
and f is negative. On
the positive parts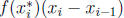 
is the area of the
rectangle whose height is
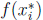and width is
.
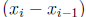On the negative parts 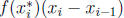is negative one times
the area of the rectangle whose height is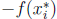 
and width is 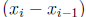. Thus the Riemann sums are the
sum of the areas of the rectangles above the x-axis
minus the sum of the areas of the rectangles below. Passing to the limit, we
conclude that can be
interpreted as the sum of the areas above the x-axis minus the areas below. The
Theorems mentioned make
sense because areas under graph of functions satisfy these properties . (You may
want to draw graphs for each
of the theorems and the corollary.)
7. Note that f(x) = x2 is increasing on [1, 2]. Thus for any
partition 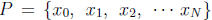of [1, 2],
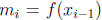and 
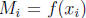. In
other words, the lower sums are obtained by using the left endpoint of the
subintervals while upper sums are obtained by using the right endpoints.
8. First observe that for any x and c in [1, 3], we have x ≥1 and c ≥1. Hence
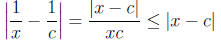
. Next note that the function is decreasing and therefore for any partition
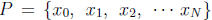of [1, 3],
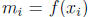and
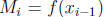. In other words, the lower sums are obtained
by using the left endpoint of the
subintervals while upper sums are obtained by using the right endpoints. Choose
N = 102 and let the above
partition be chosen so that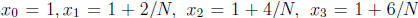 
and so on. (Note
then that
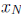= 1+2n/N = 3 as required!) Compute
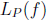and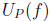 
and
subtract .
9. Show that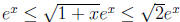 
for all x
∈ [0, 1] and integrate.
13 First note if x < c, then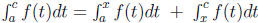 
. If f is
continuous on [a, b] then it is bounded:
say |f(t)| < M for all t in [a, b]. Let ε > 0 be given and let=
ε/M. The for all x and all c in [a, b], is
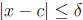and x < c, then
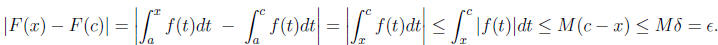
(Explain each equality and inequality in the above argument.) Give the argument
for the case if x > c.
| Prev | Next |