Elementary Functions
There are two forms of the test; both are included below.
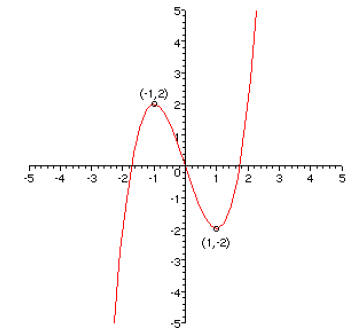
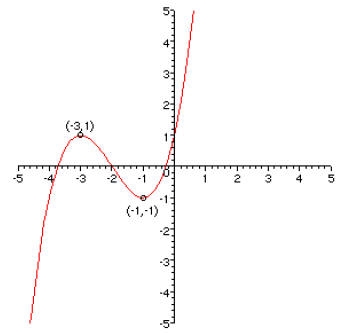
1. [20 points] On the axes on the left, graph the function f(x) = x3 – 3x. Label
the
coordinates of the points on the graph at x = ±1. Then on the axes on the right,
graph the transformed function g(x) = (1/2)f(x+2) and label the corresponding
points on this curve .
2. [15 points] The Cincinnati Enquirer (October 10, 1998)
reported that the number
of personal bankruptcies was on the rise in the late 1990’s. A good model that
fits their data is given by the quadratic function B(t) = 321t2 – 2514t + 10442.
Here, t measures years since 1990 and B(t) counts the number of personal
bankruptcies in the Tristate area in year t. Find the vertex of the parabola
which
is the graph of the function B(t). What does it tell about the number of
bankruptcies ?
The vertex has x -coordinate h = –b/2a = –(–2514)/(2*321) = 3.9 and y-coordinate
k =
B(h) = 5519.7. So the vertex is the point (3.9, 5519.7). This means that 3.9
years after
1990 (in 1994) bankruptcies in the Tristate hit an annual low of roughly 5520.
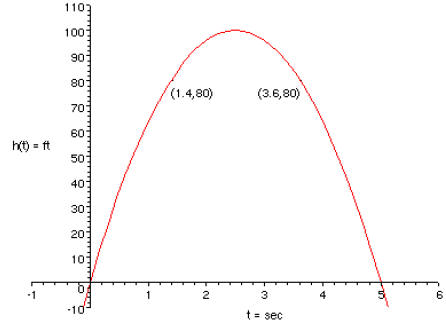
3. [15 points] A ball is thrown into the air. Its height in feet t seconds later
is given
by the equation h (t) = 80t – 16t2 Solve the equation h(t) = 80. Interpret your
solutions and illustrate them on a graph of h(t).
We solve :
( quadratic formula :) 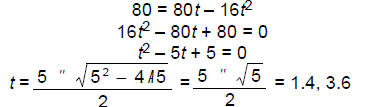
So the ball reaches a height of 80 ft twice: on the way up at t = 1.4 sec, and on the way
down at t = 3.6 sec.
4. (a) [10 points] If 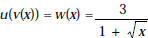 ,
find possible formulas for u (x) and v(x).
,
find possible formulas for u (x) and v(x).
There are many ways to answer this problem. Here are two different correct
answers:
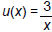 and
and 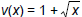 ; or
; or
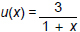 and
and 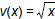 .
.
(b) [10 points] Give a formula for w -1(x).
An equation for the inverse will reverse the roles of input and output, and
solve for y :
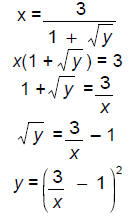
5. [15 points] Complete the table.
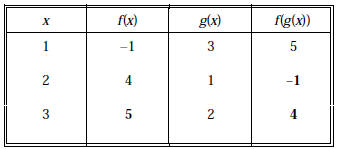
Here’s why: f(g(2)) = f(1) = –1; f(3) = f(g(1)) = 5;
f(g(3)) = f(2) = 4.
| Prev | Next |