Stability Analysis for Two Variable Systems
Stability Analysis for Two Variable Systems:
Consider a two variable model of the form

and suppose there is a point (X0, Y0) that satisfies
f(X0, Y0) = g(X0, Y0) = 0
To check the stability of this point we write
X = X0 + x and Y = Y0 + y
assumming that x and y are small. Because of this, we can expand the functions f and g as
f(X, Y) = f(X0, Y0) + Ax + By and g(X, Y) = g(X0, Y0) + Cx + Dy
where
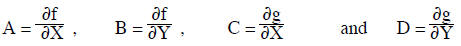
with all derivatives evalutated at the point X = X0, Y = Y0.
After this expansion the equations are of the form :
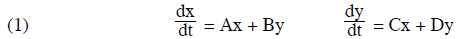
To solve these equations, we try to find a new variable

that satisfies a simpler equation

The new paramter λ is called an eigenvalue. Our job is to express α and λ in
terms of A , B, C and D.
From the definition of z, (2), and equation (3) we get
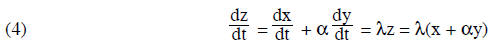
Putting in the expressions (1) for dx/dt and dy/dt this gives
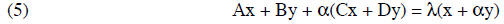
If this is going to be true for all x and all y the coefficients of x and of y must match on both sides
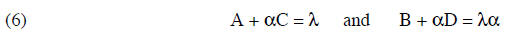
Solving the first equation for α gives

and putting this into the second equation, after multiplying by C , gives
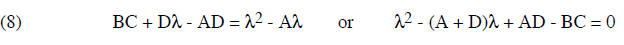
From the quadratic formula this gives
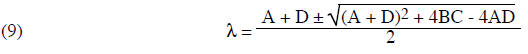
This can be simplified to
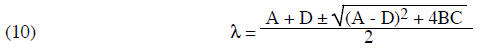
This is the main result. Note that the solution of equation (4) is

There are four possible cases: If the expression inside the square root of
(10) is positive, the λ's are
real numbers . If both λ values are negative , z (and so x and y) will decay
exponentially to zero. For
this case we must require that the larger of the two λ's is negative (case a).
If either or both of the λ's
are positive , z (and so x and y) will grow exponentially (case b). If the factor
inside the square root
is negative, the λ's are imaginary
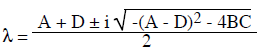
If we write λ = R + i I this means that
z(t) = z(0)exp(λt) = z(0)exp((R + i I)t) = z(0)exp(Rt)exp(iIt)
The relation
exp(iIt) = cos(It) + i sin (It)
then tells us that this produces an oscillating z (and so oscillating x and
y) with the amplitude of the
oscillations going like exp (Rt). If R = (A + D) / 2 < 0 (case c) the
oscillations will decrease to zero
while if R = (A + D) / 2 > 0 (case d) they will increase exponentially .
Summary - For

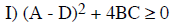
a) STABLE EXPONENTIAL
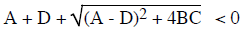
b) UNSTABLE EXPONENTIAL
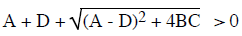
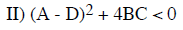
c) STABLE OSCILLATORY
A + D < 0
d) UNSTABLE OSCILLATORY
A + D > 0
| Prev | Next |