Points, Regions, Distance and Midpoints
Math 1310
Section 1.1: Points, Regions, Distance and Midpoints
In this section, we’ll review plotting points , graph
horizontal and vertical lines, some inequalities.
Develop a formula for finding the distance between two points in the coordinate
plane and one for
finding the midpoint of a line segment with given endpoints.
Graphing Points and Regions
Here’s the coordinate plane:
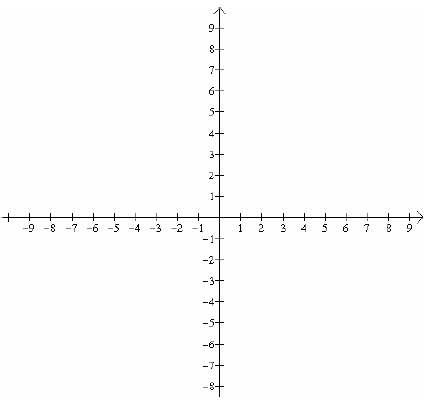
As we see the plane consists of two perpendicular lines,
the x-axis and the y-axis. These two lines separate them
into four regions, or quadrants. The pair, (x, y), is called an
ordered pair . It corresponds to a single unique
point in the coordinate plane. The first number is called the x coordinate,
and the second number is
called the y coordinate. The ordered pair (0, 0) is referred to as the
origin. The x coordinate tells us the
horizontal distance a point is from the origin. The y coordinate tells us
the vertical distance a point is
from the origin. You’ll move right or up for positive coordinates and left or
down for negative
coordinates.
Example: Plot the following points.
A. (8,6)
B. (-2,4)
C. (2,5)
D. (-3,-7)
E. (2,-3)
F. (-5,3)
Graphing Regions in the Coordinate Plane
The set of all points in the coordinate plane with y coordinate k is the
horizontal line y =k .
The set of all points in the coordinate plane with x coordinate k is the
vertical line x =k .
Example: Graph {(x, y)| x > 4 and y ≤ 3 }.
The Distance Formula
For any two points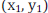 
and
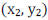, the distance between them is given by
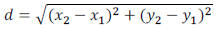
Example: Find the distance between the following pair of points.
a) (−3,1) & (1,3)
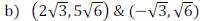
Midpoint Formula
The midpoint of the line segment joining the two points
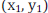) and 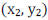is
given by
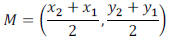
Example: Find the midpoint between the following pair of
points.
a) (−3,1) & (1,3)
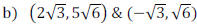
Math 1310
Section 1.2: Lines
In this section, we’ll review slope and different equations of lines. We will
also talk about x-intercept and y-intercept,
parallel and perpendicular lines.
Slope
Definition: The slope of a line measures the steepness of a line or the
rate of change of the line.
To find the slope of a line you need two points. You can find the slope of a
line between two points
and 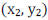by using this formula.
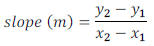
Example 1: Find the slope of the line containing the
following points
a. (4, -3) and (-2, 1)
b. (-3, 1) and (-3, -2)
Note:
-Lines with positive slope rise to the right.
-Line with negative slope fall to the right.
-Lines with slope equal to 0 are horizontal lines.
-Lines with undefined slope are vertical lines
Finding the Equation of a Line
Three usual forms:
1. Point-Slope Form
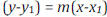
where
is a point on the line and m is the slope.
2. Slope- Intercept Form
y = mx + b
where m is the slope and b is the y-intercept of the line.
3. Standard Form
Ax + By + C = 0
where A and B are not both equal to 0.
Example 2: Write the following equation in slope-intercept form and identify the
slope and y-intercept.
2x – 4y =5
Example 3: Write an equation of the line that satisfies the given conditions.
a. m = ½ and the y-intercept is 3.
b. m = -3 and the line passes through (-2, 1).
c. line passes through (-6, 10) and (-2, 2).
Parallel Lines and Perpendicular Lines
Definition: Parallel lines are lines with slopes m1 and m2 such that they are
equal, in other words
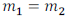
Definition: Perpendicular lines are lines in which the product of the slopes
equal -1.
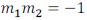
Also known as the negative reciprocal .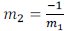 
Example 4: Write an equation of the line that passes through the points (-3, 8)
and parallel to y= −2x + 4
Example 5: Write an equation of the line that passes
through the points (1, 2) and perpendicular to
y= −2y + 4.
x-intercept and y-intercept
When graphing an equation, it is usually very helpful to find the x intercept(s)
and the y -intercepts of the
graph. An x intercept is the first coordinate of the ordered pair of a point
where the graph of the equation
crosses the x axis. To find an x intercept, let y = 0 and solve the equation for
x.
The y-intercept is the second coordinate of the ordered pair of a point where
the graph of
the equation crosses the y axis. To find a y intercept, let x = 0 and solve the
equation for
y.
Example 5: Find the x and y intercepts of the graph of the equation 3x - 4y = 8.
Example 6: Find the x and y intercepts of the graph of the equation y = x2 - 9 .
Math 1310
Section 1.3
Graphing Equations
One of the things you need to be able to do by the end of this course is to
graph several types of equations.
There are many methods to use . In this section, we’ll create a table of values
and ordered pairs, and then
plot the points in the coordinate plane. Once we have the points plotted, we can
connect the dots to get a
good picture of the equation.
Example 1: Determine which of the points (3, 2), (-1, 3) and (0, 2) are on the
graph of the equation 4x - 3y =
6.
Example 2: Determine which of the points (-1, 1), (2, -1)
and (-2, -1) are on the graph of the equation
x2+ 3xy + 2 = 0
When we graphing an equation, it will be helpful to have
more points than just the x and y intercepts of the
graph. We can create a table of values with more choices for x and find the
corresponding y values.
Example 3: Sketch the graph of the equation by plotting points: y = -3x + 2 .
Example 4: Sketch the graph of the equation by plotting points: y = x + 3
Math 1310
Section 2.1: Linear Equations
Definition: To solve an equation in the variable x using the algebraic method is
to use the rules of algebra
to isolate the unknown x on one side of the equation.
Definition: To solve an equation in the variable x using the graphical method is
to move all terms to one
side of the equation and set those terms equal to y. Sketch the graph to find
the values of x where
y = 0.
Example 1: Solve the following equation algebraically.
5y + 6 = −18 − y
Example 2: Solve following equation algebraically.
7 + 2(3 – 8x) = 4 – 6(1 + 5x)
Example 3: Solve following equation algebraically
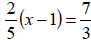
Example 4: Solve following equation algebraically.
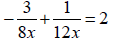
Example 5: Find the x-intercept and y-intercept of the
following equation. Express the answers in
coordinate point form.
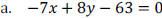
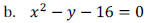
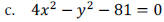
Math 1310
Section 6.1: Solving 2x2 Linear Systems
To solve a system of two linear equations
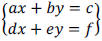
means to find values for x and y that satisfy both
equations.
The system will have exactly one solution , no solution, or infinitely many
solutions.
1. Exactly one solution, will look like:
2. No solution, will look like:
3. Infinitely many solutions, will look like:
Example 1: Solve the following systems of linear equations
by the substitution method.
2x – y = 5
5x + 2y = 8
Example 2 : Solve the following systems of linear equations by the substitution
method
x – 2y = 3
2x – 4y = 7
Example 3: Solve the following systems by the Elimination
Method .
2x + 3y = -16
5x – 10y = 30
Example 4: Solve the following systems by the Elimination Method.
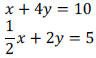
| Prev | Next |