Function Sequence and Summation

Function

• Suppose A and B are nonempty sets. A function from A to B is an assignment of exactly one
element of B to each element of A.

 – We write f: A→B.
 – We write f(a)=b if b is the element of B assigned to element a of A.

• Example:

f: Z → Z
where for each x ∈ Z, f(x)=x^2.

Domain, codomain, range

• Suppose f is a function from A to B.
 – We say A is the domain of f.
 – We say B is the codomain of f.
 – We say {f(x) | x ∈ A } is the range of f.

• Example:

f: Z → Z
where for each x ∈ Z, f(x)=x^2.
• Domain of f: Z
• Codomain of f: Z
• Range of f: {x|x=y^2, y ∈ Z}

Image and preimage

• Suppose f is a function from A to B and f(x)=y.
 – We say y is the image of x.
 – We say x is an preimage of y .
 – Note that the image of x is unique but there can be more than one preimages for y.

• Example:

f: Z → Z
where for each x ∈ Z, f(x)=x^2.
 • Image of 2: 4
 • Preimage of 4: 2
 • Another preimage of 4: -2

• Note that every element in the domain has an image.
 – But not every element in the codomain has a preimage. Only those in the range have preimages.

• Example:
f: Z → Z
where for each x ∈ Z, f(x)=x^2.
 • Each x ∈ Z has an image f(x)=x^2 .
 • But negative integers in Z do not have preimages.
 • Only perfect squares (i.e., those in the range) have preimages.

One-to-one function

• A function is one-to-one if each element in
the range has a unique preimage.
– Formally, f: A→B is one-to-one if f(x)=f(y)
implies x=y for all x ∈A,y ∈A.
• Example:

f: Z → Z
where for each x ∈ Z, f(x)=x^2.
• Clearly, f is NOT one-to-one because 4 has two preimages

Example one-to-one function

• f: N → Z
where for each x ∈ N, f(x)=x+5.
• f: Z⁺ → Z⁺
where for each x ∈ Z⁺, f(x)=x^2.
• f:{0,1,2} →{0,1,2,3}
where f(0)=1, f(1)=3, f(2)=2.

Onto function

• A function is onto if each element in
codomain has an image (i.e., codomain = range).
 – Formally, f: A→B is onto if for all y ∈B, there is
x ∈A such that f(x)=y.
• Example:
f: Z → Z
where for each x ∈ Z, f(x)=x^2.
• Clearly, f is NOT onto because 2 does not have any preimage.

Example onto function

• f: R → {0} ∪ R⁺
where for each x ∈ R, f(x)=x^2.
• f: N → Z⁺
where for each x ∈ N, f(x)=x+1.
• f:{0,1,2,3} →{0,1,2}
where f(0)=1, f(1)=1, f(2)=2, f(3)=0.

Sum of functions

• Suppose f₁, f₂, …, f_n are functions from A to R. The sum of f₁, f₂, …, f_n is also a
function from A to R defined as follows:
(f₁+ f₂+…+ f_n )(x)= f₁(x)+ f₂(x) +…+ f_n (x).
• Example:
f, g: R → R
where for each x ∈ R, f(x)=x+5; g(x)= x-3.
 • Then, f+g is defined as (f+g) (x)= 2x+2.

Product of functions

• Suppose f₁, f₂, …, f_n are functions from A to R. The product of f₁, f₂, …, f_n is also a
function from A to R defined as follows:
(f₁ f₂ … f_n )(x)= f₁(x) f₂(x) … f_n (x).
• Example:
f, g: R → R
where for each x ∈ R, f(x)=x+5; g(x)= x-3.
 • Then, f+g is defined as (f g) (x)= x^2+2x-15.

Bijection

• A function is a bijection if it is both one-to-one and onto.
• Example:
 – Consider f: Z⁺ → Z⁺ where for each x ∈ Z +, f(x)=x^2. This is NOT a bijection because it is not onto.
 – Consider f: R → {0} ∪ R⁺ where for each x ∈ R, f(x)=x^2. This is NOT a bijection either, because it is not one-to-one.
 – Consider f: R⁺ → R⁺ where for each x ∈ R⁺ , f(x)=x^2. This is a bijection.

Inverse function

• Suppose f is a bijection from A to B. The inverse function of f is the function from B to A that assigns element b of B to element a of A if and only if f(a)=b.
 – We use f^-1 to represent the inverse of f.
 – Hence, f^-1(b)=a if and only if f(a)=b.
• Example:
Consider f: R + → R⁺ where for each x ∈ R⁺ , f(x)=x^2. Its
inverse function is g: R + → R⁺ where for each x ∈ R⁺ ,
g(x)= sqrt (x).

Example inverse function

• Consider f: R + → R⁺ where for each x ∈ R⁺ , f(x)=4x+3. What is f^-1 ?

• Consider f: {0,1,2} → {0,1,2} where f(0)=1, f(1)=2, f(2)=0. What is f^-1 ?

Function composition

• Suppose g is a function from A to B, and f is a function from B to C. Then the composition of f and g is defined as:
(f o g) (x)= f(g(x)).
• Example: Consider f: R → R where for each x ∈ R , f(x)=2x+3, and g: R → R where for each x ∈ R , g(x)=3x-2.
Then, (f o g) (x)= f(3x-2) = 2(3x-2)+3=6x-1

Example composition

• Consider f: {0,1,2} →{0,1,2} where f(0)=1, f(1)=2, f(2)=0; also consider g: {0,1,2} →{1,2,3}
where f(0)=1, f(1)=2, f(2)=3.What is g o f ?

Incommutability of composition

• Consider f: R → R where f(x)=x+1, and g: R → R where g(x)=x^2.
 – It is not hard to get that f o g (x) = x^2 +1.
 – Similarly, we have that g o f (x) = (x +1)^2.
 – Clearly, f o g ≠ g o f

• In general, function composition is incommutable, which means the order of arguments in composition is important.

Graph of function

• We can often draw a graph for a function f: A → B : For each x ∈ A, We draw a point (x, f(x)).
 – Typically, we need A and B to be subsets of R.
• The graph of some important functions:
 – Linear function f(x)= kx+b : line
 – Constant function f(x) = c: line parallel to the X-axis
 – Quadratic function f(x) = ax^2+bx+c: parabola

Sequence

• A sequence is a function whose domain is a set
of integers.
– The domain is typically Z⁺ (or, sometimes, N).
– The image of n is a_n.
– Each image a_n is called a term.
– For convenience, we often write it as a₁, a₂, …, or {a_n}.
• Example:
1, 4, 9, 16, 25,… is a sequence, where the nth term is a _n =n^2 .

Example sequence

• 2, 9, 28, 65, … where the nth term is a_n =n^3 +1.
• 0, -2, -6, -12, … where the nth term is a_n = -(n-1)(n-2).
• 0, 1/2, 2/3, 3/4, … where the nth term is a_n = 1-1/n.
• -1, 1, -1, 1, … where the nth term is a_n = (-1)ⁿ.

Arithmetic sequence

• An arithmetic sequence is a sequence of the form a, a+d, a+2d, …
– Formally, it is a sequence {a_n}, where a_n =a+(n-1)d .
– Here a is called the initial term.
– Here d is called the common difference .
• Example: 9, 4, -1, -6, … is an arithmetic sequence, because it is of the form a_n = 9 -5(n- 1). The initial term is 9, and the common difference is -5.

Example arithmetic sequence

• Let x and y be two real numbers . Consider a sequence {a_n}, where a_n = 5xn +3y . Is this an arithmetic sequence?
 – The answer is yes, because we can rewrite it as a_n =(5x+3y)+5x(n-1).
 – The initial term is 5x+3y.
 – The common difference is 5x.

Geometric sequence

• A geometric sequence is a sequence of the form a, ar, ar², …
– Formally, it is a sequence {a_n}, where a_n =ar^n-1 .
– Here a is called the initial term.
– Here r is called the common ratio.
• Example: 9, 3, 1, 1/3, … is an geometric sequence, because it is of the form a_n= 9 (1/3)^n-1.
The initial term is 9, and the common ratio is 1/3.

Example geometric sequence

• Let x≠1 be a real number . Consider a
sequence {a_n}, where a_n =x²ⁿ⁺⁵ . Is this a
geometric sequence?
– The answer is yes, because we can rewrite it
as a_n =x^7 x^{^2n-2} = x^7 (x^2)^n-1 .
– The initial term is x^7.
– The common ratio is x^2.

Sum of terms

• Given a sequence {a_n}, we can sum up its mth through nth terms. We write this sum as

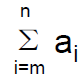
– Note it is just a simplified way to write a_m+a_m+1+…a_n . There is no difference in meaning.
– Here i is called the index of summation, m is called the lower limit of the index, and n is called the upper limit.

Sum of arithmetic sequence

• We are often interested in the sum of first n terms of a sequence. For example, consider an arithmetic sequence {a_n},

where a_n =a+(n-1)d . We have

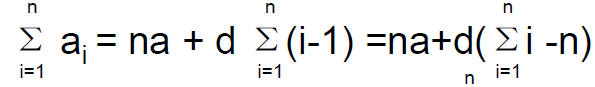
– So the main problem is to find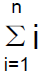

• What is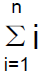

 – Let us denote it by S.
 –Recall its definition: S=1+2+…+n .
 –We can change order of terms : S= n+…+2+1.
 – Adding up the above two equations , we get 2S=(n+1)+(n+1)+…+(n+1)=n(n+1)
 –We get S=n(n+1)/2

• Now we come back to the sum of first n terms of arithmetic sequence:

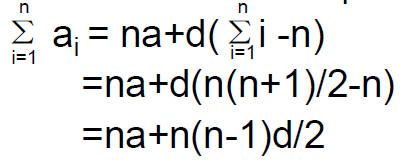
• The above is the important formula for the sum of arithmetic sequence. You should memorize it.

Example sum of arithmetic sequence

• Consider the arithmetic sequence 9, 4, -1, -6, … The sum of first n terms is

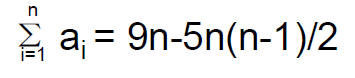
• Thus the sum of first 10 terms is

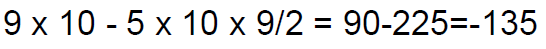
Sum of geometric sequence

• Now consider an geometric sequence {a_n}, where a_n =ar^n-1 . We have

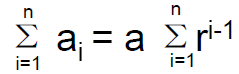
– So the main problem is to find

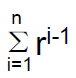
• What is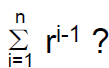

– Let us denote it by S.
– Recall its definition: S=1+R+…+r^n-1 .
– We multiply both sides by r: rS= R+…+r^n-1+rⁿ.
– Taking the difference of two equations , we get (r-1)S=rⁿ-1
– Assuming r≠1, we get S=(rⁿ-1)/(r-1) .

• Now we come back to the sum of first n terms of geometric sequence:

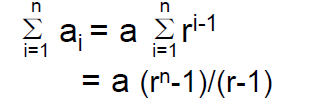
• The above is the important formula for the sum of arithmetic sequence. You should memorize it.

• Bear in mind that this formula assumes r≠1.

(Question: what is the formula for r=1 ?)

Example sum of geometric sequence

• Consider the geometric sequence 9, 3, 1, 1/3, ... The sum of first n terms is

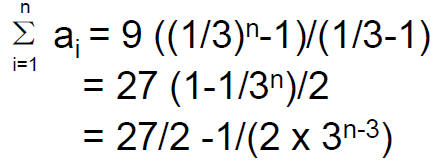
• Thus the sum of the first 5 terms is

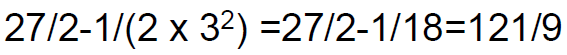
Homework 5

• Due in class Oct 21, Tuesday
• Rosen 2.3: Questions 10, 14, 18, 58, 60.
• Rosen 2.4: Questions 2, 4, 14, 16, 18.
• Optional Question (Extra Credit of 10 points):
Consider a sequence {a_n}. Denote by S_n the sum
of first n terms of this sequence. Suppose that,
for all integer n≥2, we have that a_n+2S_nS_n-1=0.
Also suppose that a₁=1/2.
(1) Prove that {1/S_n} is an arithmetic sequence.
(2) What is a_n ? Justify your answer