NUMBER SENSE: Factors of Whole Numbers

Least Common Multiple
One way to find LCM(30, 96) is to write lists of
multiples of 30 and of 96.

The least common multiple is the smallest number
common to both lists of multiples.

Multiples of 30:
30, 60, 90, 120, 150,…450, 480,
510,…,2880, 2910,…

Multiples of 96:
96, 192, 288, 384, 480, 776,…,2880, 2976,…

From these lists we see that LCM(30, 96) = 480.

However, LCM(30, 96) can also be found
using prime factorizations.
30 = 2² • 3¹ • 5¹
96 = 2⁵ • 3¹ • 5⁰

Notice that 5⁰ = 1, so the prime factorization of
96 is really 2⁵ • 3.

To find LCM’s, make sure that each prime
occurs in both lists.

To find the LCM, choose each prime raised to
the highest power from either list.

LCM(30, 96)
= 2⁵ • 3¹ • 5¹
= 480

Least Common Multiple
Worksheet

Use prime factorization to find
LCM (24, 64)
LCM(32, 48)

The characterization of GCF and LCM in
terms of prime factorization leads to:
GCF(a, b) • LCM(a, b) = a • b .

Example: GCF(30, 96) • LCM(30, 96) = 30 • 96
GCF(30, 96) = 6
LCM(30, 96) = 480

6 • 480 = 30 • 96
2880 = 2880

Using GCF(30, 96) = 6, we could have found
LCM (30, 96) as

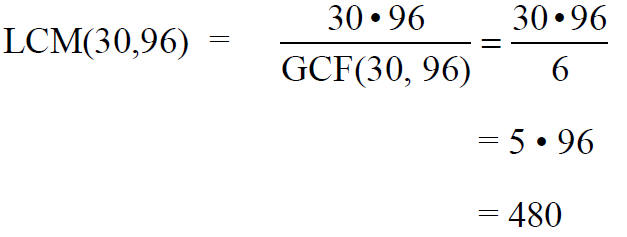
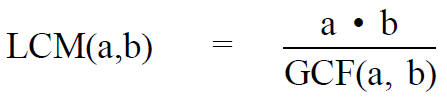
Why does
GCF(a,b ) • LCM(a,b ) = a • b ?

Consider an example:
a = 4500 = 2² • 3² • 5³
b = 4050 = 2¹ • 3⁴ • 5²

GCF(a, b ) = 2¹ • 3² • 5²
(Choose the smallest powers)

LCM(a, b ) = 2² • 3⁴ • 5³
(Choose the largest powers)

But a • b = 2² • 3² • 5³ • 2¹ • 3⁴ • 5²,
and this is the same as

GCF(a , b ) • LCM (a , b )
Both are 18,225,000

Least Common Multiples
Worksheet

Find LCM(24, 64) by applying
GCF(a, b) • LCM(a, b) = a • b.

Find LCM(32, 48) by applying
GCF(a, b) • LCM(a, b) = a • b

LEAST COMMON MULTIPLE AND
ADDITION OF FRACTIONS

Least common multiples help with the
addition of fractions.

For example

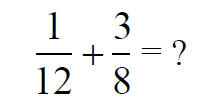
We rewrite this problem in terms of
equivalent fractions with a common
denominator.

One possible choice for a common
denominator is 8 • 12,

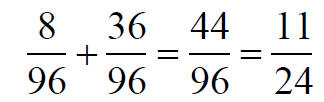
Or,
by using LCM(12, 8) = 24

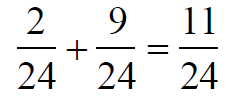
Addition of Fractions
Worksheet

Find the sums for the following fractions
by using the least common denominator.

Sample Word Problems

Try these problems:
1. Two joggers are running around a track.
One jogger runs a lap in 6 minutes and
the other takes 10 minutes. If they start at
the same time and place, how long will it
take for them to meet at the starting place
at the same time.

2. A 48 member band follows a 54 member
band in a parade. If the same number of
players must be in each row of both
bands, what is the largest number of
players that can be placed in each row?
Assume each row has the same number of
players.

Answers:
1. LCM(6, 10) = 30
2. GCF(48, 54) = 6

Enrichment
Determining Whether a Number is Prime
For a number that is not a perfect square,
factors occur in pairs. To determine whether a
number is prime, it is not necessary to check
all smaller numbers as possible factors.
Is 137 prime?

For any pair of factors whose product is 137,
one of the factors would be less than .

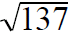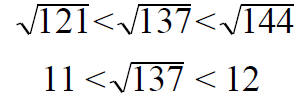
It is sufficient to confirm that the numbers
2, 3, 4, 5, 6, 7, 8, 9, 10, and 11
are not factors of 137
to show that 137 is prime.

In fact, it is not necessary to check all whole
numbers between 1 and 11.

E.g., if 6 were a factor of 137,
its prime factors (2 and 3)
would also be factors of 137.

We only need to check that the primes <
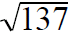
2, 3, 5, 7, and 11
are not factors of 137.

To establish that a is prime,
it is sufficient to confirm that
all primes less than or equal to
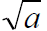
fail to be factors of a.

Checking Whether a Number is Prime
Worksheet

What is the smallest list of numbers that must be
checked as possible factors of 223?

Is 223 prime?

What is the smallest list of numbers that must be
checked as possible factors of 179?

Is 179 prime?

Divisibility Rules
Basic ingredients:
“A|B” means “A divides B or in other words,
there is an integer k such that
B = A • k.

Proof: If A|B , there is an integer k₁, such that
B = A • k₁. If A|C, there is an integer
k₂ such that C = A • k₂.

Therefore:
B + C
= A • k₁ + A • k₂
= A (k₁ + k₂)

So, A|(B + C)

Proof: If A|(B+C), B + C = A • k₁ , for some
integer k₁ . If A|C, C = A • k₂ for some integer
k₂. Then
B = (B + C) – C
= A • k₁ – A • k₂
= A (k₁ – k₂)
Therefore A|B.

Divisibility by 2
2|(a •10² + b • 10 + c ) if and only if 2|c.

The only single digit numbers divisible by 2
are 0, 2, 4, 6, and 8.

Therefore, 2|(a • 10² + b • 10 + c) if and only
if c = 0, 2, 4, 6, or 8.

Divisibility by 3
3|(a • 10² + b • 10 + c ) if and only if
3|(a + b + c )

Proof:
a • 10² +b • 10 + c
= a • (99 + 1) + b • (9 + 1) + c
= (a • 99 + b • 9) + (a + b + c)

Let B = a • 99 + b • 9. Then 3|B
Because B = 3 • (a • 33 + b • 3).

Let C = a + b + c . If 3|C , then 3|(B + C) by
Theorem 1. If 3|(B +C ) then 3|C by Theorem
2.

Example: 3|129 because 3|(1+2+9)