Fundamental Computer Concepts of Informatics
Today:
Probabilistic Analysis
Geometric and Binomial Distributions
The Simplified Hiring Problem assumes:
• You are running a company and want to hire a better office assistant
• You don’t want to fire your current assistant until you know you have a better
assistant
• You ask an employment agency to send one candidate each day (n total
candidates)
• You make the decision whether or not to hire the new assistant and fire the
old assistant
immediately after interviewing the new candidate
• The cost to interview a candidate is ci, and the cost to hire a new candidate
is ch (where ch >> ci)
Task: You want to know the expected cost of the process if you interview n candidates
Hire_Assistant(n)

Here, n is the # of candidates interviewed and m is the # of candidates hired
Total Cost: 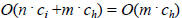
(since 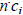 is the the cost to interview n
candidates, we are more interested in
is the the cost to interview n
candidates, we are more interested in 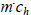 which
varies
which
varies
according to how many people are hired)
Worst-case: 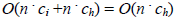
(every new candidate is better than previous assistant )
We want to analyze the expected m ( number of candidates hired)
• Assume the candidates arrive in random order
• Define a random variable X which indicates the number of assistants hired
during the process
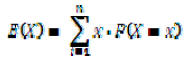
(but this is somewhat difficult to calculate since the order of candidates must be known apriori)
So, let’s define an indicator random variable Xi
associated with the event in which the ith
candidate is hired
Xi = I {candidate i is hired} =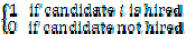
and
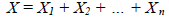
taking the expectation of both sides we have,
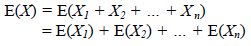
we also know
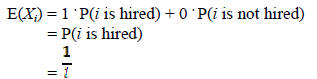
so
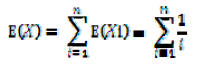 (i.e. sum of a harmonic
series)
(i.e. sum of a harmonic
series)
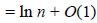
Therefore the expected cost of hiring a candidate is :
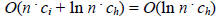
The Birthday Paradox
Task: Anticipate how many people must there be in a
room such that the expected number of pairs of
people that have the same birth month and day is at least 1
Assumptions:
• Ignore leap years for simplicity
• Index the people in the room from 1 to k
• Assume people are equally likely to have their birthdays on any day of the
year
• Let bi be the birthday of the ith person
Since birthdays are assumed to be independent of each
other, the probability that two people (i and j) have
birthdays is:
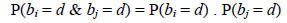
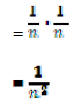
where
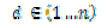
therefore
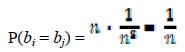
We will define the indicator random variable Xij:
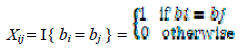
so
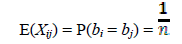
let X be the random variable that counts the pairs of people with the same birthday
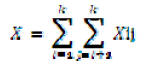
Taking the expectation of both sides
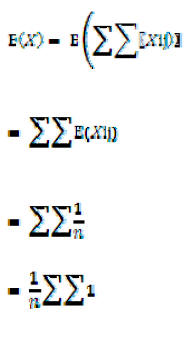
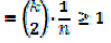
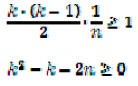
using the quadratic formula
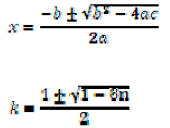
When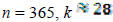 , so
, so
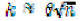
Geometric and Binomial Distributions
Bernouli Trial - an experiment with only 2 possible
outcomes
• P(success): p
• P(failure): q = 1 - p
We want to consider multiple Bernouli trials, and we
assume that each repeat of the trial is independent
from the previous trial.
For example: roll a die, where only a 6 is considered a success
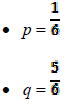
Geometric Distribution : what is the probability that the first success occurs in the kth trial?
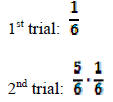
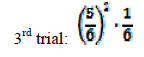
So,
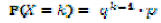
To find the expectation of distribution, assuming q < 1
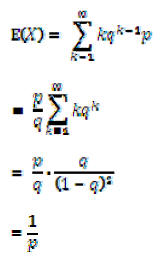
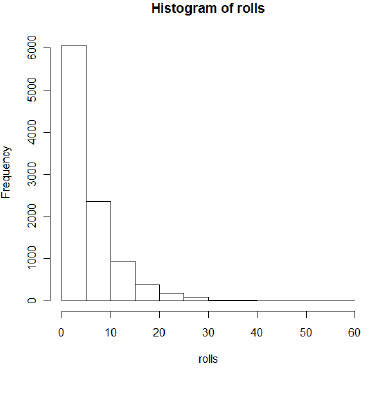
Sample geometric distribution
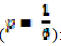
Binomial Distribution : how many successes occur during n Bernouli trials?
P(success) = p
P(failure) = q = 1 - p
So,
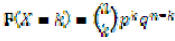
and
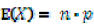
and
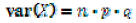
Sample binomial distribution
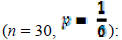
| Prev | Next |