Graphing Linear Equations and Inequalities
|
5.1 The Rectangular Coordinate System The rectangular coordinate system (figure 1) has four quadrants created by intersecting a horizontal and a vertical number line . The horizontal number line is called the horizontal axis, often labeled the x-axis. The vertical number line is called the vertical axis, often labeled the y-axis. When the axes intersect at their zero points , the point of intersection is called the origin. The quadrants are labeled in a counterclockwise direction with Quadrant I in the upper-right, Quadrant II in the upper-left, Quadrant III in the lower-left, and Quadrant IV in the lower-right. |
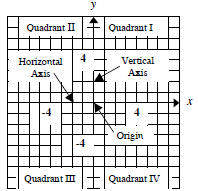
Figure 1 The rectangular |
|
The location of every point in the rectangular coordinate system is identified by a pair of numbers called an ordered pair (x, y). The first component of an ordered pair is called the abscissa (often referred to as the x-coordinate); it is the horizontal distance from the point to the y-axis. The second component of an ordered pair is called the ordinate (often referred to as the y-coordinate); it is the vertical distance from the point to the x-axis. The graph or plot of a point in the plane is a dot placed at the location given by the ordered pair of the point. For example, to graph the ordered pair (4, 2) place a dot 4 units to the right and 2 units up from the origin (0, 0). See figure 2. Try graphing the point (2, 4) in figure 2. |
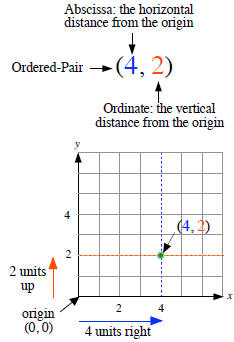
Figure 2 To graph the ordered pair (4, 2), |
Example 1
Graph the following ordered pairs. Label each point and
identify the quadrant each
point lies in.
|
1. A(2, 5) and B(5, 2) 2. C(3, -6) and D(-6, 3) 3. E(4, 0) and F(0, 4) 4. G(-5, -3) and H(-3, -5) |
 |
Example 2
Identify the ordered-pair location of each point on the
graph.
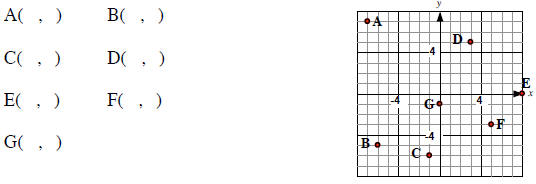
5.1.2 Scatter Diagrams
A scatter diagram is the graph of known ordered-pair data. A
scatter diagram illustrates the visual relationship between the two
variables in the ordered pair.
Example 2
A study by the Federal Aviation Administration showed that narrow,
over-the-wing emergency exit rows slow passenger evacuation. The
table below shows the space between seats, in inches, and the
evacuation time for 35 passengers. Graph the scatter diagram for the
data.
|
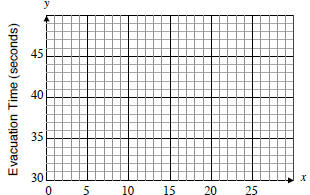 Space Between Seats (inches) |
5.1.3 Average Rate of Change
Given two ordered -pairs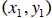 
and
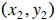the average rate of
change (ARC) of y with respect to x is given by
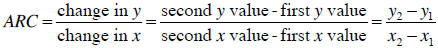
Example 3
From the data in example 3, find the average rate of change (ARC)
using the points (6, 44) and (20, 37). Analyze the units of the ARC to
interpret your results.
5.2 Graphs of Linear Equations (Straight Lines)
5.2.1 Linear Equations in Two Variables in the form
y =mx +b
A linear equation in two variables is any equation whose graph
forms a straight line. One form of a linear equation in two variables is
y = mx + b, where x and y are the variables, m is the [constant]
coefficient of x , and b is also a constant. A second form will be
discussed in the next section.
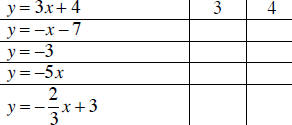
Example 1 For each equation, identify the constants m and b.
| Equation, y = mx + b | m | b |
 |
||
Solution to a Linear Equation in Two Variables
A solution to a linear equation in two variables is an ordered pair
of numbers (x, y) that [when substituted for the variables ] makes the
equation true.
Example 2 Is (3, -5) a solution to y = -3x + 4?
Example 3 Is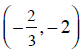 
a
solution to y = -3x + 4?
5.2.2 Graphs of Linear Equations in the form y =mx +b
Equations with two variables have an infinite number of ordered-pair
solutions. The graph of an equation in two variables is a drawing
of all the ordered-pair solutions to the equation. The graph of every
linear equation in two variables (i.e.y = mx + b) forms a straight line.
Graphing Linear Equations by Plotting Three Points
To graph a linear equation in the form y = mx + b:
1. Pick three values for x.
2. For each x chosen in step 1, use the given equation, y = mx + b, to
compute the three corresponding values of y .
3. Plot the three ordered pairs and use a ruler to draw a straight line
through the points. Draw the line through the entire grid and draw
arrowheads at each end of the line to show that the line continues
indefinitely.
|
Example 5 Graph y = 2x - 3 by finding three solutions. |
 |
|
Example 6 Graph y = -3x + 2 by finding three solutions. |
|
|
Example 7 Graph 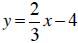 byfinding three solutions. |
|
|
Example 8 Graph 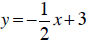 byfinding three solutions. |
|
| Prev | Next |