Information and Logic
S is the set of all the words in English
A web page is an element in the algebra

The Second Edition of the Oxford English Dictionary
contains
full entries for W? words in current use, and
M? obsolete words
The Second Edition of the Oxford English Dictionary
contains
full entries for 171,476 words in current use, and
47,156 obsolete words.
1/n words are nouns, 1/v verbs,
and 1/a adjectives
A search is finding all the subsets (web pages) that
consistent with the subset defined by the query
A query is an element in the algebra
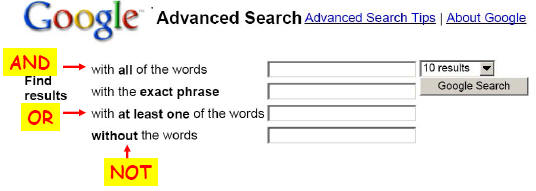
Examples of Boolean Algebras
• 0-1 ( two valued ) Boolean algebra
OR / AND
• Arithmetic Boolean algebras (Boolean integers)
lcm / gcd
• Algebra of subsets = any Boolean algebra
union / intersection
An Amazing Theorem
Representation Theorem (Stone 1936):
Every finite Boolean algebra is isomorphic to a Boolean
algebra of subsets of some finite set S.
| Algebra 1 | Algebra 2 | |
| elements |  |
elements |
| operations /elements |  |
operations /elements |
Marshall Stone
| Marshall Stone 1903-1989
|
Proved in 1936 90AB = years After Boole The Boolean Syntax invented in 1847 has a unique representative semantic!!! |
| Marshall entered Harvard in 1919 intending to continue his studies at Harvard law school ; fell in love with Mathematics , and the rest is history… |
|
| Harlan Fiske Stone 12th Chief Justice of the US 1941-1946 |
|
| Marshall had a passion for travel. He began traveling when he was young and was on a trip to India when he died.... |
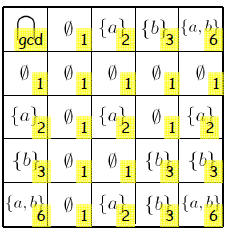
Arithmetic Boolean Algebras
Isomorphic to Algebra of Subsets
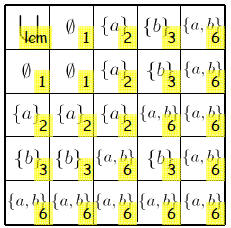
The set of divisors of a Boolean integer
{1,2,3,6}
The operations : lcm and gcd
The special elements: 1 and 6
Isomorphic to: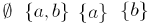 |
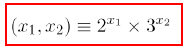
Arithmetic / Subsets
An Amazing Theorem
Representation Theorem (Stone 1936):
Every finite Boolean algebra is isomorphic to a Boolean
algebra of subsets of some finite set S.
Two Boolean Algebras with m elements are isomorphic
Every Boolean algebra has 2k elements
Provides intuition beyond the axioms:
We can 'naturally' reason about results in Boolean algebra
Algebra of Subsets
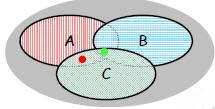 |
Venn Diagram John Venn 1834 - 1923  |
| graphical representation of all possible subsets |
 |
 Correcting Errors
Correcting Errors
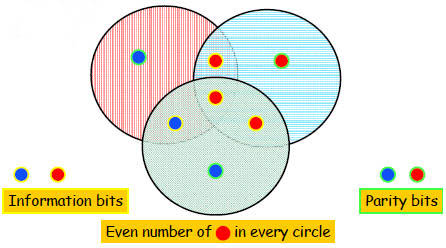
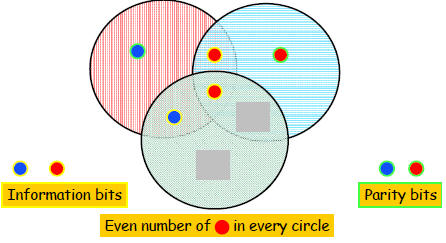
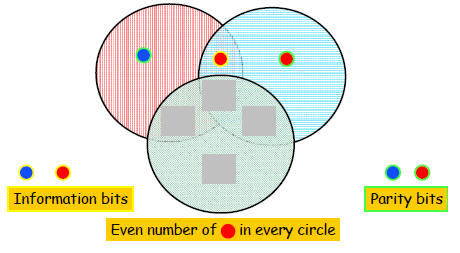
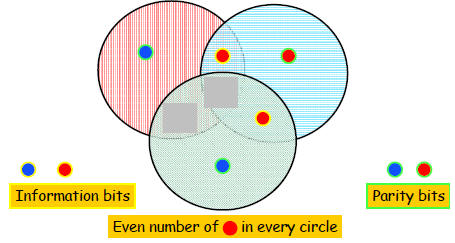
Three erasures are not correctable...
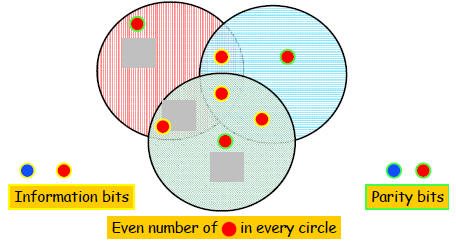
Is one error correctable?
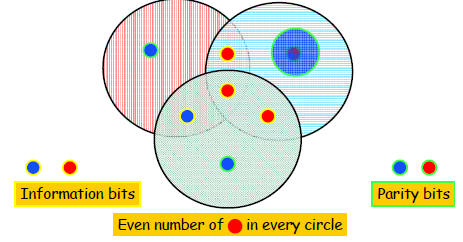
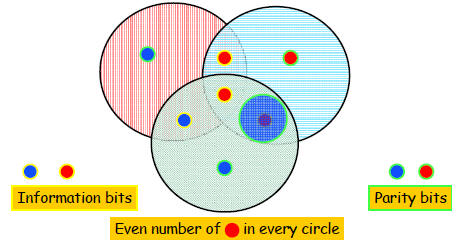
The First nontrivial Code
| Richard Hamming 1915-1988
|
 |
| Prev | Next |

