Matrix Operations on a TI -83 Graphing Calculator

(This paper is based on a talk given in Spring Semester 2004.) The use of a graphing calculator can
be useful and convenient, especially when reducing a matrix that has entries with many decimal
places. The inverse of a matrix can also be found easily. One of the homework assignments for
MAT 119 is to reduce a matrix with a graphing calculator.

Introduction

Two important applications with matrices in MAT 119 are solving a system of linear equations and finding
the inverse of a matrix. The TI series of graphing calculators is able to find the inverse and put a matrix in
reduced row echelon form automatically, but students still should learn how to do row operations, especially
when using the Simplex Method in Chapter 4. The purpose of this paper is to indicate the appropriate steps.

A brief word on notation. When a box is drawn around a symbol, that means to press that key on
the TI. Hence means to push the multiplcation button . If two key presses are used, they will be to
refer to functions printed in different colored keys on the calcuator. The keypresses will be given, along
with the operation to be performed, the latter in slanted type and in brackets. For instance,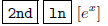
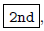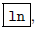means to press then and this accesses the function ex; this is in yellow ink on the TI-83. Also,
[A] puts the calculator in alphabetic mode and enters the letter A in the display; these letters
are printed in green ink on the TI-83.

Solving A System of Linear Equations

Suppose you want to solve the system.

25x + 61y - 12z = 10
18x - 12y + 7z = -9
3x + 4y - z = 12

Here's how to solve it.

1. Enter the augmented matrix into the calculator.

Press to put the calculator in MATRIX mode.
You now see a list of matrix names down the left-hand side of the screen, and the words NAMES,
MATH and EDIT across the top, with NAMES currently "highlighted." Pressing the right-arrow key
or will change which word is highlighted. Pressing will select the name of the matrix you
want to enter. Let's enter the system above into the matrix A; move the cursor to the right so that EDIT
is highlighted (press if you haven't moved the highlighted part) and press
You are now prompted to enter the dimensions of the matrix A; enter the number of rows
and the number of columns The TI-83 can handle matrices with up to 99 rows and/or columns,
but cannot handle a matrix with both due to limited memory.

NOTE. At any time, if you realize you made a mistake, you can press 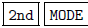[QUIT] and then start over.
Now you need to enter the coefficients and numbers on the right hand side. The cursor is placed in the first
row, first column of the matrix. If you type in a number (or an expression) and hit it will put that
number into the matrix and move to the next position, to the right (if you're not at the right-most column)
or down to the first column of the next row. After entering a number in the last row and last column, the
cursor stays there.

So we need to put in the coefficients. The keystrokes for this are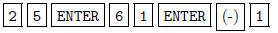
etc.

2. Perform the row operations.

Now you need to get back to the calculation mode. Press 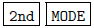[QUIT]. You are ready to perform
row operations on your matrix A.

The first thing we will do is to swap the first and third rows of A. Press 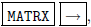then twelve
times; the cursor should be next to a command called rowSwap(. Press , which will bring you back
to the "calculation mode." Now you need to enter the matrix. press 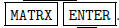. (If you want to do a
row reduction on a matrix other than A, you need to "scroll down" by pressing repeatedly.) Then press

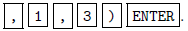
This gives you the matrix 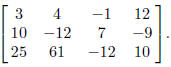If you need to see columns further to the right of
the screen, press the key.

NOTE. Doing row operations on A will not change the value of A on a TI -83, so we will need to keep
track of the new matrix. We will do this by using the ANS command. It is also a good idea
to copy onto paper the matrix we get at this point, in case we have to go back to it.

Now we want to divide the first row by 3, so that there is a 1 in the upper left corner. Press
which will display *row( in the calculator. We want to multiply the first row of ANS by
1/3, so we type in. 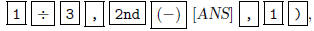then The matrix we get is

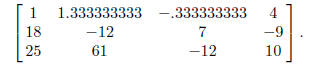
(Don't worry about the decimal approximation; we'll x it at the very end.)
Now you need to subtract 18 times Row 1 from Row 2, to turn the entry in the 2nd row, 1st column
into a 0. Enter.
The new matrix is

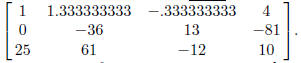
Now, you perform these same types of row operations over and over. The key sequences are below.

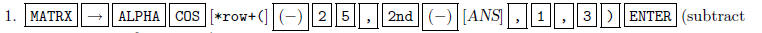
25 times row 1 from row 3).

row 2 by -36).

3.
(subtract 27.666666667 times row 2 from row 3).

4. If you press repeatedly, you will find that the entry in the 3rd row and 3rd column is approximately
6.32407407407. This is what you want to divide row 3 by.

5. The matrix is now in row echelon form. To get it into reduced row echelon form, continue with.

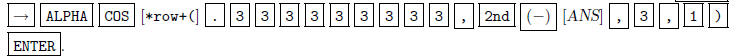
Now the matrix is close to reduced row echelon form; the entries on the main diagonal are very close to
1, and the other entries in the first three columns are close to zero. Press or hold the until you can see
the fourth column of the matrix. The value in the first row is x = 4.566617845, the value in the second row
is y = -6.443631037, and the value in the third row is z = -24.07467057.

You can try to convert these decimals to fractional form by typing in [ANS]
[!Frac] In this case, it doesn't help - the TI-83 only tries fractions with denominators less than
or equal to 100 - but it may in others.

Inverting a Matrix

Inverting a matrix can be done on the TI without as much work; it is built-in to the calculator. Here we
will invert the matrix

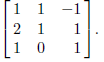
1. Enter the matrix into the calculator.
This can be done as in the previous section; put it into matrix B, then press 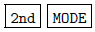[QUIT] to get
back into "calculation mode."

2. Calculate the inverse.

Type in. 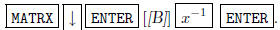You get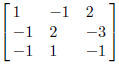, after a few seconds have gone by.
Other matrix computations are possible. For instance, to find 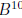, type
the answer is

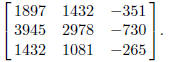
Matrix Operations on a TI-85 Graphing Calculator

(This paper is based on a talk given in Spring Semester 2004.) The use of a graphing calculator can
be useful and convenient, especially when reducing a matrix that has entries with many decimal
places. The inverse of a matrix can also be found easily. One of the homework assignments for
MAT 119 is to reduce a matrix with a graphing calculator.

Introduction

Two important applications with matrices in MAT 119 are solving a system of linear equations and finding
the inverse of a matrix. The TI series of graphing calculators is able to find the inverse and put a matrix in
reduced row echelon form automatically, but students still should learn how to do row operations, especially
when using the Simplex Method in Chapter 4. The purpose of this paper is to indicate the appropriate steps.

A brief word on notation. When a box is drawn around a symbol, that means to press that key on
the TI. Hence means to push the multiplcation button. If two key presses are used, they will be to
refer to functions printed in different colored keys on the calcuator. The keypresses will be given, along
with the operation to be performed, the latter in slanted type and in brackets. For instance,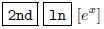
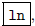means to press , then and this accesses the function ex; this is in yellow ink on the TI-85. Also,
[A] puts the calculator in alphabetic mode and enters the letter A in the display; these letters
are printed in blue ink on the TI-85.

Solving A System of Linear Equations

Suppose you want to solve the system.

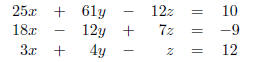
Here's how to solve it.
1. Enter the augmented matrix into the calculator.

Press [MATRX] to put the calculator in MATRIX mode.
You will see five "words" above the keys through NAMES, EDIT, MATH, OPS, CPLX. To
enter a matrix, press the key under EDIT You are now asked for the name of the matrix, which can
be any single letter. The cursor is in alphabetic mode, so all you have to do is press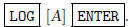
You are now prompted to enter the dimensions of the matrix A; enter the number of rows
and the number of columns The TI-85 can handle matrices with up to 99 rows and/or columns,
but cannot handle a matrix with both due to limited memory.

NOTE. At any time, if you realize you made a mistake, you can press and then start over.
Now you need to enter the coefficients and numbers on the right hand side. The cursor is placed in the first
row, first column of the matrix. If you type in a number (or an expression) and hit it will put that
number into the matrix and move to the next position, to the right (if you're not at the right-most column)
or down to the first column of the next row. After entering a number in the last row and last column, the
cursor stays there.

So we need to put in the coefficients. The keystrokes for this are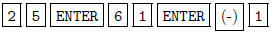
etc.

2. Perform the row operations.

Now you need to get back to the calculation mode. Press . You are
ready to perform row operations on your matrix A.

The first thing we will do is to swap the first and third rows of A. Press the key to get the
following "words" above the keys through aug, rSwap, rAdd, multR, and mRAdd. To swap two
rows, press [rSwap(]. Now you need to type the rest in. the name of the matrix (press ALPHA LOG
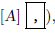and the two rows to be swapped (press

This gives you the matrix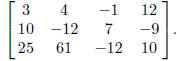 If you need to see columns further to the right of
the screen, press the key.

NOTE. Doing row operations on A will not change the value of A on a TI-85, so we will need to keep
track of the new matrix. We will do this by using the ANS 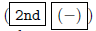command. It is also a good idea
to copy onto paper the matrix we get at this point, in case we have to go back to it.
Now we want to divide the first row by 3, so that there is a 1 in the upper left corner. We are still have the
options aug, rSwap, rAdd, multR, and mRAdd, so we can just press 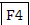[multR(]. We want to multiply the first
row of ANS by 1/3, so we type in. 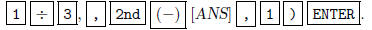The matrix we get is

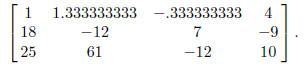
(Don't worry about the decimal approximation; we'll x it at the very end.)
Now you need to subtract 18 times Row 1 from Row 2, to turn the entry in the 2nd row, 1st column
into a 0. Enter. F5 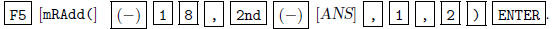The new
matrix is

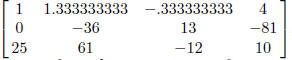
Now, you perform these same types of row operations over and over. The key sequences are below.

1. 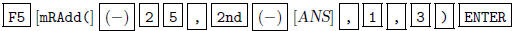(subtract 25 times row 1 from
row 3).
2. [multR(] 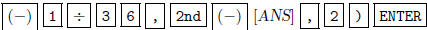(divide row 2 by -36).
3. [mRAdd(]
(subtract 27.6666666667 times row 2 from row 3).
4. If you press repeatedly, you will find that the entry in the 3rd row and 3rd column is approximately
6.32407407409. This is what you want to divide row 3 by. [multR(]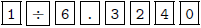

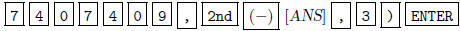
5. The matrix is now in row echelon form. To get it into reduced row echelon form, continue with.
[mRAdd(]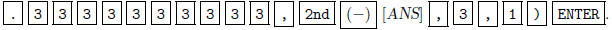

Now the matrix is close to reduced row echelon form; the entries on the main diagonal are very close to
1, and the other entries in the first three columns are close to zero. Press or hold the until you can see
the fourth column of the matrix. The value in the first row is x = 4.56661786066, the value in the second
row is y = -6.44363103925, and the value in the third row is z = -24.074670571.

You can try to convert these decimals to fractional form by typing in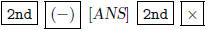
[MATH] 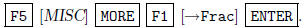In this case, this only gives you an exact value for z,
namely -16443=683. The TI-85 only tries fractions with denominators less than or equal to 1000, so you
may get exact values in other situations. Note that roundo errors kept us from getting exact answers for x
(3119/683) and y (-4401=683).

Inverting a Matrix

Inverting a matrix can be done on the TI without as much work; it is built-in to the calculator. Here we
will invert the matrix

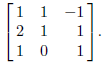
1. Enter the matrix into the calculator.
This can be done as in the previous section; put it into matrix B, then press to get back into
"calculation mode."

2. Calculate the inverse.

Type in.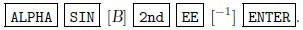 You get 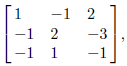after a few seconds have
gone by.

Other matrix computations are possible. For instance, to find 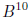, type
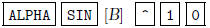
the answer is