Inverse Functions

Overview

• Section 4.1 in the textbook:
– Introduction to Inverse Functions
– Graphing Inverse Functions
– Composition of a Function and Its Inverse
– Finding Inverse Functions

Introduction to Inverse
Functions

Inverses & One-to-one Functions

• Recall that for each point in a function:
– Each x- coordinate is associated with only ONE
y-coordinate

• Given a function f consisting of a set of points,
let f^-1 denote the relation that results if we swap
the x and y coordinates of each point in f

• If f^-1 is also a function, then it is called the
inverse of f AND f is classified as a one-to-
one function
– Ex: f = {(0, 0), (1, 5), (-3, 4)}→ f^-1 = {(0, 0), (5, 1),
(4, -3)} →f is a one-to-one function

• The domain and range of a function and its
inverse are switched:
– Ex: f = {(0, 0), (1, 5), (-3, 4)} →
f^-1 = {(0, 0), (5, 1), (4, -3)} →
f (domain) = {-3, 0, 1} & f (range) = {0, 4, 5} →
f^-1 (domain) = {0, 4, 5} & f^-1 (range) = {-3, 0, 1}

• To test a graph for an inverse, we use the
horizontal line test
– If the horizontal line
crosses the graph
more than once, the
graph does not
have an inverse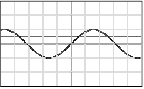

Inverses & One-to-one Functions
(Example)

Ex 1: Determine whether each function has
an inverse. If the function does not have
an inverse, state why:

a) {(0, 0), (1, 1), (4, 2), (9, 3), (16, 4)}
b) {(-2, 4), (-1, 1), (0, 0), (1, 1), (2, 4)}

Ex 2: Determine which graphs have an
inverse: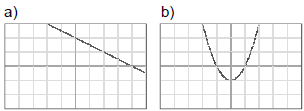

Graphing Inverse Functions

Graphing Inverses

• Given the equation of f AND that f is a
one-to-one function, we can sketch a
graph of f^-1

– Swap the x and y coordinates of f

• The graph of f and its inverse f^-1 is
symmetric to the line y = x
– If we folded a piece of paper over the line
y = x, f and f^-1 would lie on top of each other

Graphing Inverses (Example)

Ex 3: Given the graph of f (x), sketch f^-1 (x),
the inverse of f (x):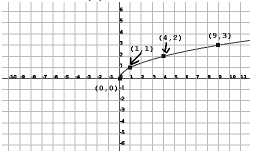

Composition of a Function and
Its Inverse

Composition of a Function and Its
Inverse

• Suppose we start off with the value 8
– If we multiply 8 by 2, we get 16
– If we divide 16 by 2, we get back to the original 8
– Works the same way if we divide first and then
multiply

• Multiplication & division are inverse operations
– One undoes the effect of the other

• Recall that a composition takes the output of
one function as the input to another
– In our case, the output of the first “function” was a
product which was then put into a division “function”

• Given a one-to-one function f, f^-1 is the
inverse of f if and only if
– (f ◦ f^-1 )(x) = x
• The composition of f and f^-1 yields the original
value

• AND
– (f^-1 ◦ f) (x) = x

• The composition of f^-1 and f yields the original
value

Composition of a Function and Its
Inverse (Example)

Ex 4: Determine whether the given functions f
and g are inverses: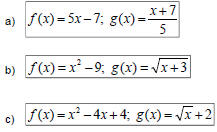

Finding the Inverse of a
Function

Finding the Inverse of a Function

• Rather than a graph of f^-1 , we more often than
not want the equation of f^-1

• Recall that to find f^-1 when f consisted of a set of
points, we switched the x and y coordinates

• Given that f is a one-to-one function, to find f^-1 :
– Replace f (x) with y
– Switch x and y
– Solve for y
– Substitute f^-1 (x) for y

• Remember how to check whether two functions
are inverses

Ex 5: Given that the function is one-to-one, find
its inverse: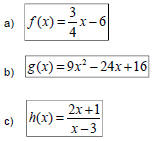

Summary

• After studying these slides, you should know how to do
the following:

– Understand the concept of an inverse function
– State whether a function has an inverse by looking at its
graph
– State the domain and range of a function and its inverse
– Graph the inverse of a function
– State whether two functions are inverses by using
composition
– Find the inverse of a function

• Additional Practice
– See the list of suggested problems for 4.1

• Next lesson
– Exponential Functions (Section 4.2)