MATH 153 - FINAL EXAM
1. Do not open this exam until you are told to begin.
2. This exam has 11 pages including this cover. There are 8 questions.
3. Do not separate the pages of the exam.
4. Please read the instructions for each individual exercise carefully. One of
the skills being tested on
this exam is your ability to interpret questions, so I will not answer questions
about exam problems
during the exam.
5. Show an appropriate amount of work for each exercise so that the I can see
not only the answer but
also how you obtained it. Include units in your answers where appropriate.
6. You may use your calculator . However, please indicate if it is used in any
significant way .
7. If you use graphs or tables to obtain an answer, be certain to provide an
explanation and sketch of
the graph to make clear how you arrived at your solution .
8. Please turn o all cell phones.
| PROBLEM | POINTS | SCORE |
| 1 | 14 | |
| 2 | 16 | |
| 3 | 12 | |
| 4 | 10 | |
| 5 | 12 | |
| 6 | 15 | |
| 7 | 6 | |
| 8 | 15 | |
| TOTAL | 100 |
1. (2 points each) Circle "True" or "False" for each of the following
problems. Circle "True" only
is the statement is always true. No explanation is necessary.
(a) Two vectors in three-space are parallel if and only if their cross product is 0.
True False
(b) The smaller the radius of a circle, the larger the curvature of the circle .
True False
(c) The dot product of two vectors is another vector.
True False
(d) The series
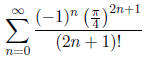 converges.
converges.
True False
(e) The equation (u*v) + (v*w) makes sense.
True False
(f) The vectors i + j and 2i-2j are orthogonal.
True False
(g) One has (u*v)*v = 0 for all vectors u and v.
True False
2. (4 points each) Let u = 2i + 3j - 4k and v = -i + j - 4k.
(a) Find 2u + v.
(b) Find u*v.
(c) Find |u| and |v|.
(d) What is the angle between u and v?
3. (4+6 points) As the holidays approach you decide to rearrange the
furniture in your living
room to accomodate more people. You decide to push your couch into a new
location 3 meters
away from its current position. You push downward on the couch at an angle of 35
degrees with
a force of 200 N for 20 seconds and are unable to budge the couch. (The 35
degrees is the angle
between your force and the horizontal.)
(a) How much work have you done on the couch?
(b) A friend stops over and helps by pulling the couch while you push at the
same angle with the
same force as before. Together you are able to move the couch into the new
position. How much
work have YOU done on the couch this time?
4. (6 points each) (a) Find the equation of the plane through (1, 2, 3) and
perpendicular to the
vector w = i + 2j + 3k.
(b) Find the equation of the plane through (-1,-2, 3) and perpendicular to
both the planes
x - 3y + 2z = 7 and 2x - 2y - z = -3.
5. (3 points each) Suppose that the function f(x) has the degree 12 Taylor
polynomial centered
at x = 3 given by
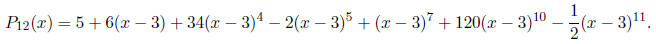
Suppose that we know that
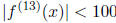 for all 0 < x < 10.
for all 0 < x < 10.
(a) What is the slope of the tangent line to f(x) at x = 3?
(b) What is the value of
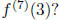
(c) Using the Taylor polynomial given, give an approximation of f(3.5).
(d) Bound the error obtained in part (c).
6. (3 points each) Twelve inches of water sit in your sink. A foolish little
bug lands on the surface
of the water just as you release the drain. The bug's path along the water
rushing from the sink
can be modelled by the vector
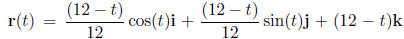 where t is
where t is
measured in seconds and distances are measured in inches.
(a) What is the bug's initial position?
(b) At what time does the bug reach the drain and how did you arrive at this answer?
(c) At time t = π seconds, what is the bug's velocity?
(d) At time t = π seconds, what is the bug's speed?
(e) What is the curvature of the bug 's path at t = π seconds? The following may be helpful:
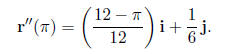
7. (6 points) Three people decide to slice up a pie into 4 equal pieces, each
of them removing a
quarter of the pie. They then slice up the remaining quarter of the pie into 4
equal pieces, each
of them removing a quarter. They continue slicing up and removing the remaining
part in this
way. Show that each person ends up with one third of the pie in the end.
8. (3+4+4+4 points) Consider the circle of radius a centered at (a, 0).
(a) Write the Cartesian equation for this circle.
(b) Show that one can write the equation from part(a) as r = 2a cos(θ).
(c) A goat is tethered to the edge of a circular pond of radius a by a rope
of length ka (0 < k ≤ 2).
Graph on the axes below the grazing area of the goat. Be sure to label your
graph appropriately.
(Hint: This was exactly a homework problem. The pond is represented by the
circle from part
(a). The rope should sweep out a circle of radius ka.)
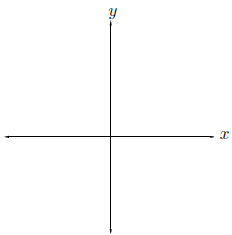
(d) Find the grazing area of the goat.
Theorem 1. (Integral Test) Let f be a continuous, positive,
nonincreasing function on the interval
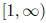 and suppose that ak = f(k) for all positive integers k. Then the infinite series
and suppose that ak = f(k) for all positive integers k. Then the infinite series
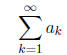
converges if and only if the improper integral
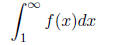
converges.
Theorem 2. (p-series) The series
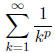
converges if p > 1 and diverges if p≤1.
Theorem 3. (Ordinary Comparison Test) Suppose that
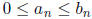 for all n≥N.
for all n≥N.
(i) If
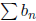 converges, so does
converges, so does
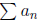 .
.
(ii) If
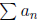 diverges, so does
diverges, so does
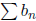 .
.
Theorem 4. (Limit Comparison Test) Suppose that
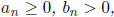 and
and
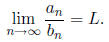
If
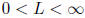 ,
then
,
then
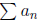 and
and
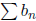 converge of diverge together. If L = 0 and
converge of diverge together. If L = 0 and
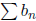 is convergent,
is convergent,
then
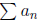 converges.
converges.
Theorem 5. (Alternating Series Test) Let
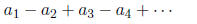
be an alternating series with
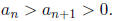 If
If
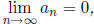 then the series converges. Moreover,
then the series converges. Moreover,
the error made by using the sum S n of the first n terms to approximate the sum S of
the series
is not more than an+1.
Theorem 6. (Absolute Ratio Test) Let
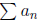 be a series of nonzero terms and suppose that
be a series of nonzero terms and suppose that
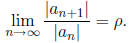
(i) If 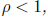 the series
converges absolutely (hence converges).
the series
converges absolutely (hence converges).
(ii) If 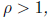 the series diverges.
the series diverges.
(iii) If 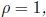 the test is inconclusive.
the test is inconclusive.
Some Potentially Useful Formulas
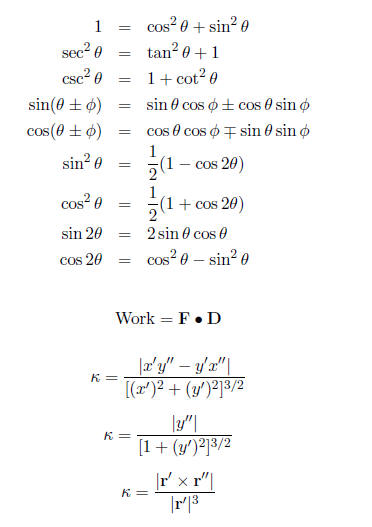
| Prev | Next |