COLLEGE ALGEBRA, EXAM TWO
There are eight partial credit problems on this exam. Show
all your work on the page on
which the question appears.
Problem 1 (10 points). Find a linear function f(x) such
that the graph of y = f(x) passes
through the points (1,-2) and (4, 4) in the xy- coordinate plane .
Solution . Write f(x) = mx + b. Set x1 = 1, y1 = -2, x2 = 4, and y2 = 4.
Use the slope formula to find m.
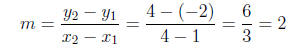
So f(x) = 2x + b. Since the graph of y = f(x) passes
through (1,-2), we get f(1) = -2.
2(1) + b = -2,
2 + b = -2,
b = -2 - 2 = -4
Therefore f(x) = 2x - 4.
Problem 2 (10 points). Find a linear function f(x) such that f(-1) = 2 and the
graph of
y = f(x) is perpendicular to the straight line x - y = 2 in the xy-coordinate
plane.
Solution . Write f(x) = mx + b.
(1) Find the slope of the straight line x - y = 2. Solve x - y = 2 for y.
x - y = 2,
y = x - 2,
slope = 1
(2) The straight lines y = f(x) and x - y = 2 are perpendicular to each other.
m ۰ 1 = -1,
m = -1
So f(x) = -x + b.
(3) Since f(-1) = 2, we get -(-1) + b = 2 or b = 1.
Therefore f(x) = -x + 1.
Problem 3 (17 points). Questions (a) through (d) refer to the quadratic function
y = 2x2 - 4x - 2 :
(a) Complete the square for y = 2x2 - 4x - 2.
Solution. In this quadratic function , a = 2, b = -4, and c = -2.
Write
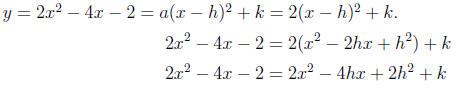
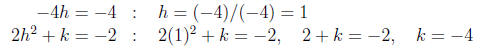
Therefore y = 2(x - 1)2 - 4.
(b) Find the x- and y- intercepts on the graph of y = 2x2 - 4x - 2.
Solution. (1) Find the x-intercepts.
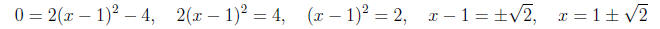
(2) Find the y-intercept.
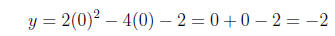
x-Intercept(s):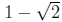 and
and
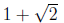
y-Intercept: -2
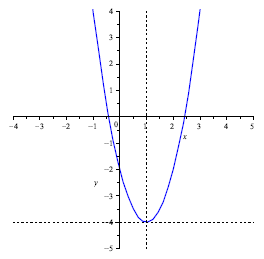
(c) Graph the function y = 2x2 - 4x - 2. Specify the
vertex and the axis of symmetry.
The axes are marked o® in one-unit intervals.
Vertex : (1,-4)
Axis of Symmetry: x = 1
(d) Determine whether the function y = 2x2 - 4x - 2 has
the maximum value or the
minimum value .
 Maximum Value
Maximum Value
 Minimum Value
Minimum Value
Problem 4 (10 points). A point P(x, y) lies on the graph of the function y = x2
- 1.
Express the distance from P(x, y) to the origin O(0, 0) as a function of x.
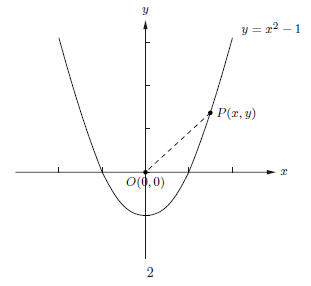
Solution. Let d be the distance from P(x, y) to O(0, 0). By the distance formula , we get
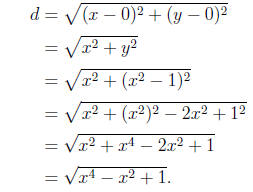
Problem 5 (14 points). Suppose that the height of a
baseball thrown straight up is given
by the function
H(t) = -16t2 + 64t
where H is in feet and t is in seconds.
(a) Find the maximum height that the baseball can reach.
Solution. H(t) = -16t2 + 64t is a quadratic function with a = -16, b = 64, and c
= 0.
Write
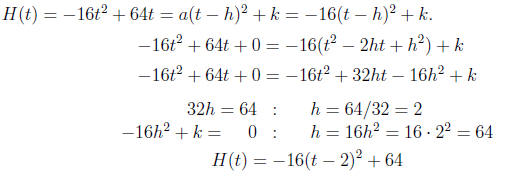
Answer: The maximum height that the baseball can reach is 64 feet.
(b) Find the time at which the baseball hits the ground.
[ Hints: The height of the baseball is 0 feet when it hits the ground. ]
Solution. Find the time t when H(t) = 0.
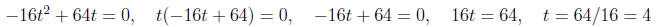
Answer: The baseball hits the ground at the time t = 4 seconds.
Problem 6 (12 points). Questions (a) and (b) refer to the polynomial function
y = -(x - 1)3 - 2 :
(a) Find the x- and y- intercepts on the graph of y = -(x - 1)3 - 2.
Solution. (1) Find the x-intercept.
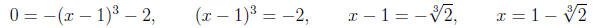
(2) Find the y-intercept.
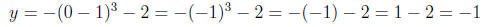
x-Intercept(s):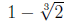
y-Intercept: -1
(b) Graph the function y = -(x - 1)3 - 2. The axes are
marked off in one-unit intervals.
Solution. Steps :
(1) Sketch the graph of y = x3.
(2) Reflect the graph of y = x3 about the x-axis to get the graph of y = -x3.
(3) Shift the graph of y = -x3 to the right by 1 unit to get the graph of y =
-(x-1)3.
(4) Shift the graph of y = -(x-1)3 down by 2 units to get the graph of y =
-(x-1)3-2.
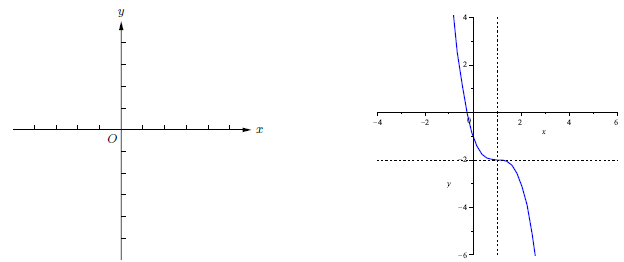
Problem 7 (14 points). Questions (a) through (c) refer to
the polynomial function
y = (x + 2)(x - 1)(x - 3) :
(a) Determine the x- and y-intercepts on the graph of y = (x + 2)(x - 1)(x - 3).
Solution. (1) Find the x-intercepts.
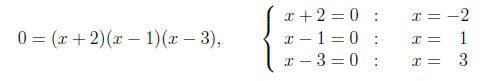
(2) Find the y-intercept.
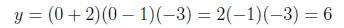
x-Intercept(s): -2, 1, and 3
y-Intercept: 6
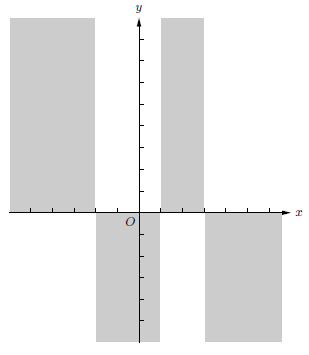
(b) Sketch the excluded regions for the graph of y = (x +
2)(x - 1)(x - 3). The axes are
marked off in one-unit intervals.
Solution. Determine the signs of y = (x + 2)(x - 1)(x - 3).

The excluded regions are the shaded regions in the following figure.
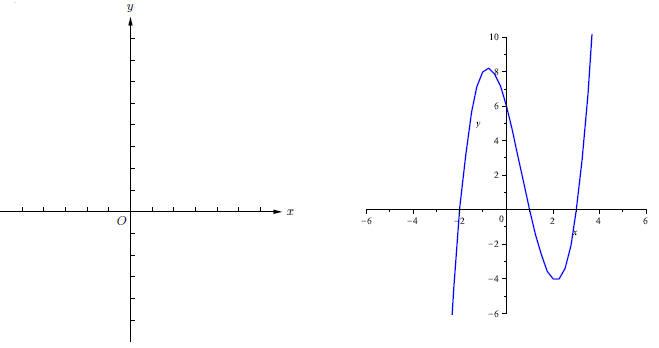
(c) Sketch the graph of y = (x + 2)(x - 1)(x - 3). The
axes are marked off in one-unit
intervals.
Solution.
Problem 8 (13 points). Questions (a) through (c) refer to the rational function
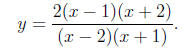
(a) Write out the domain of the function
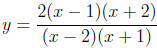 in
interval notation.
in
interval notation.
Solution. This function is defined when (x - 2)(x + 1) ≠ 0.
Domain: (-∞,-1) ∪ (-1, 2)
∪ (2,∞)
(b) Find the x- and y-intercepts on the graph of
Solution. (1) Find the x-intercepts.
(2) Find the y-intercept.
x-Intercept(s): -2 and 1 y-Intercept: 2 (c) Find the horizontal and vertical asymptotes to the
graph of
Solution. Use the approximation method to determine the
horizontal asymptote.
Horizontal Asymptote: y = 2 Vertical Asymptote(s): x = -1 and x = 2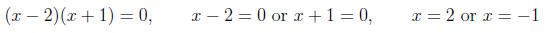
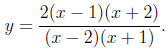
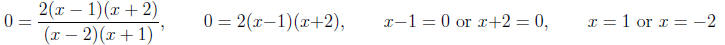
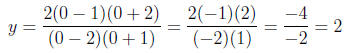
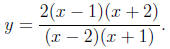
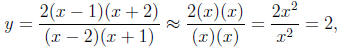 when
|x| is very large.
when
|x| is very large.
| Prev | Next |