Simplify a Fraction
•To Simplify a Fraction divide out of top and bottom any
common factors.
( Numbers that are divisible by both numerator and denominator.) You
must divide out all such common factors for a fraction to be simplified.
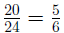 divide 4 out of the top (numerator) and
bottom (denominator)
divide 4 out of the top (numerator) and
bottom (denominator)
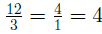 divide 3 out of the top (numerator) and
bottom (denominator)
divide 3 out of the top (numerator) and
bottom (denominator)
*Note 1: Sometimes when working problems involving fractions it may be
useful to put an integer over 1 (since 2 = 2/1 you have not changed the prob
lem).
*Note 2: For all operations involving fractions do not work with mixed numbers.
First change them to improper fractions then follow the rules below .
Mixed Number to Improper Fraction
1. Multiply the denominator times the whole number then add on the numerator
(ignore the sign).
2. Place this number over the denominator and attach the sign. Example:
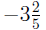
5 · 3 + 2 = 17 step one
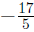 step two
step two
Improper Fraction to Mixed Number
1. Divide the denominator into the numerator. Ask yourself how many
times the denominator will go into the numerator?
2. This is the whole number. The remainder is the numerator. The denominator
is the same.
Example: 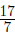
| goes into 17 2 times with 3 left over | step one |
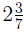 |
step two |
Adding or Subtracting Fractions
You must have a common denominator
1. If you do not have a common denominator find the LCM of the numbers
in the denominator.
2. Multiply the denominator by the number that will get you to the LCM.
Also, multiply the numerator by that same number. (Whatever you do
to the bottom of the fraction you must do to the top.) Repeat with the
other fraction.
3. Add or Subtract the numerators and place the answer over the common
denominator.
4. Simplify if possible.
Example: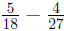
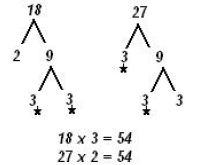
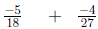 |
Change the subtraction to addition by adding the opposite |
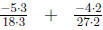 |
Multiply the denominator by the number that will get you to the LCM. (notice the number you multiply by is just the un-starred prime factors of the other numbers.) |
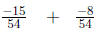 |
Multiply |
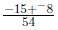 |
Place over the common denominator |
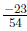 |
Add and see if there is the fraction can be simplified. |
Multiplying Fractions
NO common denominator needed
Method 1
1. Divide out of top and bottom any common factors (this can be directly
below or within another fraction but never top with top or bottom with
bottom).
2. Multiply across the top (numerator) and multiply across the bottom
(denominator)
3. Be sure to check your sign and double check to make sure it is completely
simplified.
Example: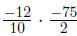
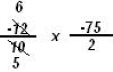 |
divide by 2 top and bottom |
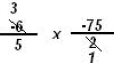 |
divide by 2 top and bottom |
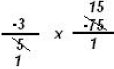 |
divide by 5 top and bottom |
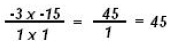 |
multiply across the top and bottom and simplify |
Multiplying Fractions
NO common denominator needed
Method 2
1. Replace all the numbers with their prime factorizations.
2. Cancel common factors in the top and bottom (this can be directly below
or within another fraction but never top with top or bottom with
bottom).
3. Multiply across the top (numerator) and multiply across the bottom
(denominator)
4. Be sure to check your sign and double check to make sure it is completely
simplified.
Example: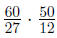
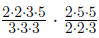 |
find the prime factorizations of all the numbers |
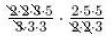 |
cancel common factors |
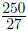 |
multiply across the top and bottom remember to check the sign |
Dividing Fractions
Never Divide Fractions. Change it to multiplication.
• Changing to multiplication
1. leaving the first number alone
2. change the ÷ to ×
3. change the second number to its reciprocal (flip it)
4. follow the rules of multiplication
• Example: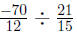
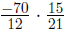 |
Leave the first alone, multiply and flip |
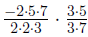 |
find the prime factorizations of all the numbers |
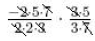 |
cancel common factors |
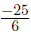 |
multiply across the top and bottom remember to check the sign |
Inequalities
Symbols
> greater than 3 > 2
< less than 2 < 34
≥greater than or equal to 3 ≥2 also 3 ≥3≤ greater than
or equal to 2 ≤3
also 3 ≤3
Determining Symbol
1. Simplify each side using appropriate rules
2. Place numbers on a number- line if necessary
3. Choose an appropriate symbol (often there can be more than one symbol
mentioned that will work.)
Example: −|3 − 6| ?? − 2 · 2
−|3 − 6| = −|3| = −3 Simplify the left-hand side
−2 · 2 = −2 · 2 = −4 Simplify the right-hand side
So, −3≥ −4 and −3 > −4 are both correct
Properties and How to Identify Them
• Commutative Property of Addition
a + b = b + a
Identify by first looking at the order in which the numbers are coming.
If there is a change, see if the order is switched around addition.
• Commutative Property of Multiplication
a × b = b × a
Identify by first looking at the order in which the numbers are coming.
If there is a change, see if the order is switched around multiplication.
• Associative Property of Addition
a + (b + c) = (a + b) + c
First, identify if different numbers are grouped together. If yes, does it
involve addition.
• Associative Property of Multiplication
a(b · c) = (a · b)c
First, identify if different numbers are grouped together. If yes, does it
involve multiplication.
• Additive Identity
a+0 = a so 0 is the additive identity since when it is added to a number
it equals that number.
• Additive Inverse
a + (−a) = 0 The additive inverse is the opposite of a number because
when you add it you get back the identity (0).
• Multiplicative Identity
a · 1 = a so 1 is the multiplicative identity since when it is multiplied by
a number it equals that number.
• Multiplicative Inverse
a(1/a) = 1 The additive inverse is the reciprocal of a number because when
you add it you get back the identity (1).
• Distributive Property
a(b + c) = ab + ac or a(b − c) = ab − ac
3(1 + 2) = 3 · 1 + 3 · 2
Combining Like Terms
1. Identify the like terms (Terms are separated by + or - signs. Like terms
are those that have exactly the same variable.)
2. Identify the coefficients of your like terms (These are just the numbers
attached to the variable.) For 4x2 and −5x2 they are 4 and
−5 respectively.
3. Add the coefficients.
4. Attach the common variable.
Note: the coefficient of x is understood to be 1.
The term with no variable is considered the constant term.
Example: 4x2 − 3x + 2 − 5x2 + x + 7,
| 4x2and − 5x2 | are like terms |
| −3x and x | are like terms |
| 2 and 7 | are like terms |
| Note: the subtraction attaches itself to the number to the right of it. |
|
| 4x2 − 5x2 | 4 and − 5 are the coefficients. |
4x2 − 5x2 = −1x2 = −x2 |
since 4 + (−5) = −1 |
The other like terms follow similarly
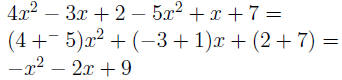
Solving Equations (Basics)
1. Simplify both sides of the equation first. (Distribute and combine like
terms.)
2. Decide which side you want the variable to be on.
3. Add the opposite to get the numbers on one side and the variable term
on the other.
4. Divide both sides by the coefficient of the variable.
5. Make sure your answer is simplified.
Example: Solve 2 − 5(x + 3) = 7(x − 1)
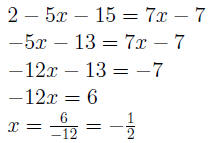 |
Distribute on either side of the equality. Combine like sides on either side of equation. Add −7x to both sides Add 13 to both sides Divide both sides by −12 and simplify. |
Solving Equations (With Fractions)
1. Simplify both sides of the equation first. (Distribute and combine like
terms.)
2. Find the Least Common Denominator
3. Multiply everywhere by the Least Common Denominator
4. Cancel where possible. (All fractions should now be gone.)
5. Decide which side you want the variable to be on.
6. Add the opposite to get the numbers on one side and the variable term
on the other.
7. Divide both sides by the coefficient of the variable.
8. Make sure your answer is simplified.
Example: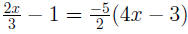
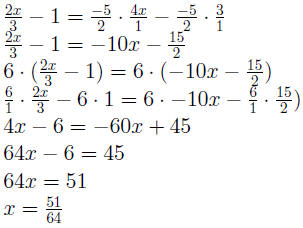 |
Distribute Simplify Multiply by LCD (6) Distribute Simplify Add 60x to both sides Add 6 to both sides Divide by 64 on both sides Check to see if it simplifies |
Word Problems
• “Math” Words (these group and keep in order of wording)
1. Sum: The sum of a number and two.
Math Translation: (x + 2)
2. Difference: The difference of a number and two.
Math Translation: (x − 2)
3. Product: The product of a number and two.
Math Translation: (x · 2)
4. Quotient: The quotient of a number and two.
Math Translation: (x ÷ 2)
• “Normal” language (tends to place out of order and does not group)
1. More: Three more than a number.
Math Translation: x + 3
2. Less: Three less than a number.
Math Translation: x − 3
3. Subtract from: Subtract three from a number.
Math Translation: x − 3
• The verb in the sentence often indicates the equality
• Use the above hints to translate the problem into math.
• Be sure to solve the equation if asked to do so.
• Example: The product of 3 and the difference of a number and 1 is
the same as subtracting 5 from the twice number. Find the number.
(3 · (x − 1)) = 2x − 5
| Prev | Next |