Multiplying Polynomials
Omit: Multiplying vertically and Examples 9 & 10
Review: product rule , distributive property , monomial, binomial, polynomial
Objective 1: Multiply two polynomials
To multiply a monomial by a monomial we will use the product rule covered in
section 5.1.
Note, we do not need to have like terms to multiply, just to add/subtract.
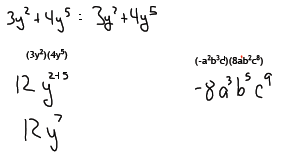
To multiply a monomial by a binomial or longer polynomial we use the
distributive
property
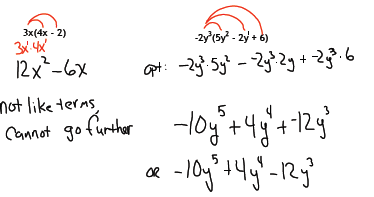
Objective 2: Multiply two binomials
To multiply two polynomials we need to multiply each term of the first
polynomial by
each term of the second polynomial.
When multiplying a binomial by a binomial (something we will do a lot) a handy
process to use is the FOIL method .
First, Outside, Inside, Last.
We will need to combine like terms for our final answer.
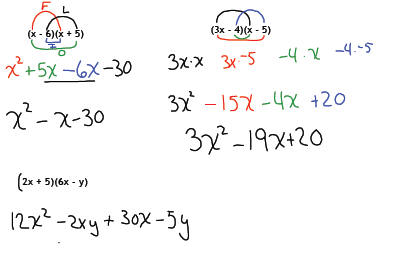
Objective 3: Squaring Binomials
There are two ways to square (multiply by itself) a binomial: (a + b)2.
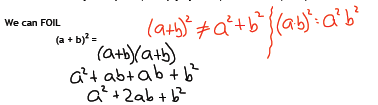
Or we can memorize this formula and use it in place of FOIL when you need to
square
a binomial.
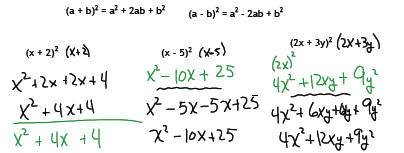
If you have difficulty remembering the formulas, you can always use FOIL to
square a
binomial.
Warning! A very common error is
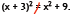
Not true!
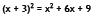
Objective 4: Multiplying the sum and difference of two terms
Here is another pattern that will come up often. Again you can either memorize
the
formula or use the FOIL method.
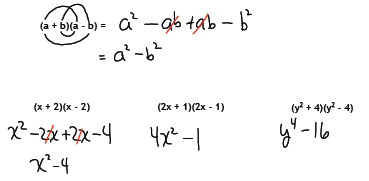
Formula summary:
FOIL: First, Outside, Inside, Last
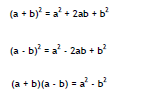
Section 5.5: Greatest Common Factor and Factoring by Grouping
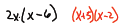
Our goal is to rewrite polynomial expressions as being products of factors
rather
than sums of terms.

Review: The difference between factors and terms
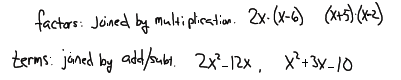
Objectives 1& 2: Identify and factor out the Greatest Common Factor (GCF)
Factoring is “un‐multiplying” 6 = 2 * 3
so 2 and 3 are factors of 6, and 2*3 is the factored form of 6.
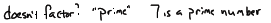
The factored form of
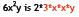
the factored form of

The factors common to both monomials are
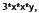 so the GCF
is
so the GCF
is
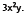
To factor out a GCF from a polynomial, we determine the GCF of the
polynomial’s
terms and “un‐distribute” the GCF.
Our goal is the have an expression equivalent to the original polynomial, but
an
expression that is a product of a monomial (the GCF) and a simpler polynomial.
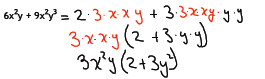
Note that if we were to multiply our result, we would have exactly what we
started
with so this is an equivalent expression but written in a different format .
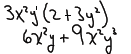
Note also that 2 + 3y2 have no common factors.
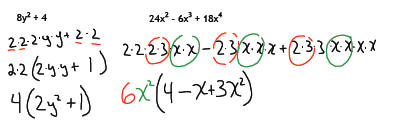
Note: for the first example, the 1 is not optional!
Without having the 1 as a
placeholder, we would not have an equivalent expression…the second term of the
polynomial would be lost.
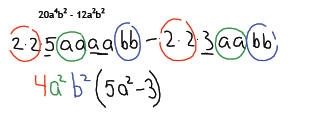
Can there be more than one correct factorization of a
polynomial?
There can be depending on the sign :
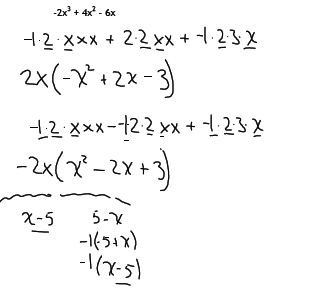
| Prev | Next |