Introduction to Elementary Number Theory
Integer division
• Let a be an integer and d be a positive integer . Then
there are unique integers q and r (0 ≤r<d), such that
a=dq+r.
– We can view the above procedure as the division of a by d .
– q is called the quotient of this division. We write q=a div d.
– r is called the remainder of this division. We write r = a mod d.
– If r=0, then we say d divides a , and write d | a.
• Example: We divide 13 by 3, and get that 13 = 3 X 4 +1.
So, 13 div 3=4 and 13 mod 3 =1.
Since the remainder is not 0, we say that 3 does not
divide 13.
Example for integer division
• Divide 27 by 5. What is the quotient and
what is the remainder?
• Does 14 divide 98?
• Divide 1000 by 333.
• Does 1111 divide 2345?
Basic properties of division
Theorem: Let a, b, c be integers. Then:
(1) If a | b and a | c, then a | b+c.
(2) If a | b, then a | bc for all integers c.
(3) If a | b and b | c, then a | c.
Proof: (1) Let d= b div a and d'= c div a.
Then b+c= da+d'a=(d+d')a. So a | b+c.
(2) Let d= b div a. Then bc=adc. So a | bc.
(3) Let d= b div a and d'= c div b. Then
c=d'b=d'da. So a | c.
Example for properties of division
• Suppose a, b, c are integers such that a |
b and a | c. Show that, for all integers m, n,
a | mb+nc.
Proof: Let d= b div a and d' = c div a. Then
mb+nc= mda+nd'a
=(md+nd')a.
So, a | mb+nc.
• Note you should memorize this result.
Congruence
• Let a and b be integers, and m be a
positive integer . Then we say a is
congruent to b modulo m if a mod m = b
mod m.
– We write a ≡ b (mod m).
• Example:
13 mod 4 = 1 = 21 mod 4.
So, we have 13 ≡ 21 (mod 4).
Equivalent definition for congruence
Theorem: Let a, b be integers and m be a positive
integer. Then a ≡ b (mod m) if and only if m | ab.
Proof: (1) First, we show that, if m | a-b, then a ≡
b (mod m). We let q= a div m, r= a mod m; q'=b
div m, r'= b mod m. So, a= mq+r and b=mq'+r'.
Without loss of generality, assume r≥ r'. Hence,
r-r' ≥0. Since r-r'≤r<m, we have 0 ≤r-r'<m.
On the other hand, a-b=(mq+r)-(mq'+r')=m(qq')+(
r-r'). So, r-r' = a-b mod m=0, which implies
that r=r'. Hence, a ≡ b (mod m).
(2) Next, we show that, if a ≡ b (mod m),
then m | a-b. We let q= a div m, r= a mod
m; q'=b div m, r'= b mod m. So, a= mq+r
and b=mq'+r'. Furthermore, a ≡ b (mod m)
means r=r'.
Hence, a-b=(mq+r)-(mq'+r')=m(q-q')+(rr')=
m(q-q'), which means m | a-b.
Example for congruence
• Is 101 congruent to 91 modulo 9?
• 101 ≡ 91 (mod ???)
• 100 ≡ 99 (mod ???)
Addition of congruence
Theorem: Let m be a positive integer. If a ≡ b (mod m)
and c ≡ d (mod m), then a+c ≡ b+d (mod m).
Proof: Let r= a mod m and r'=c mod m. Since a ≡ b (mod
m) and c ≡ d (mod m), we have r= b mod m and r'=d
mod m.
Now let p= a div m, q= b div m, p'= c div m, q'= d div m. So,
a=pm+r, b=qm+r, c=p'm+r', d=q'm+r'. Hence, (a+c)-(b+d)
= (pm+r+p'm+r') - (qm+r+ q'm+r')=(p+p'-q-q')m, which
means m | (a+c)-(b+d). By the equivalent definition of
congruence, a+c ≡ b+d (mod m).
Example for addition of congruence
• 10001+20000005+3004 ≡? (mod 10 )
Solution : 10001≡1 (mod 10)
20000005 ≡5 (mod 10)
3004 ≡ 4 (mod 10)
So,
| 10001+20000005+3004 | ≡ 1+5+4 (mod 10) |
| ≡ 10 (mod 10) | |
| ≡ 0 (mod 10) |
Multiplication of congruence
Theorem: Let m be a positive integer. If a ≡ b (mod m)
and c ≡ d (mod m), then ac ≡ bd (mod m).
Proof: Let r= a mod m and r'=c mod m. Since a ≡ b (mod
m) and c ≡ d (mod m), we have r= b mod m and r'=d
mod m.
Now let p= a div m, q= b div m, p'= c div m, q'= d div m. So,
a=pm+r, b=qm+r, c=p'm+r', d=q'm+r'. Hence, ac-bd =
(pm+r)(p'm+r') - (qm+r)(q'm+r')=(pp'+pr'+p'r-qq'-qr'-q'r)m,
which means m | ac-bd. By the equivalent definition of
congruence, ac ≡ bd (mod m).
Example for multiplication of congruence
• 10001 X 20000005 ≡? (mod 10 )
Solution : 10001≡1 (mod 10)
20000005 ≡5 (mod 10)
So,
| 10001 X 20000005 | ≡ 1X 5 (mod 10) |
| ≡ 5 (mod 10) |
Addition and residue
Theorem: Let m be a positive integer and a, b
be integers. Then,
(a+b) mod m = ((a mod m)+(b mod m)) mod m.
Proof: Clearly, we have a ≡ a mod m (mod m),
and b ≡b mod m (mod m). So, we get that
a+b≡(a mod m) + (b mod m) (mod m),
which is equivalent to that
(a+b) mod m = ((a mod m)+(b mod m)) mod m.
Multiplication and residue
Theorem: Let m be a positive integer and a,
b be integers. Then,
ab mod m = ((a mod m)(b mod m)) mod m.
The proof is analogous to the previous
theorem and so we skip it here.
Example for calculating residue
• What is 20082008 mod 3 ?
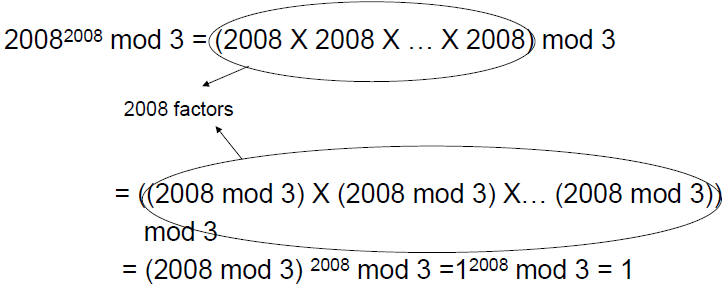
| Prev | Next |