Inverse Functions

Objective: In this lesson you learned how to find inverse functions
graphically and algebraically .

I. Inverse Functions (Pages 237-238)
For a function f that is defined by a set of ordered pairs , to form
the inverse function of f, . . .

What you should learn
How to find inverse
functions informally and
verify that two functions
are inverse functions of
each other

For a function f and its inverse f^-1, the domain of f is equal to
___________________, and the range of f is equal to
___________________.

To verify that two functions , f and g, are inverse functions of
each other, . . .

Example 1: Verify that the functions f (x) = 2x - 3 and
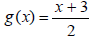are inverse functions of each other.

II. The Graph of an Inverse Function (Page 239)
If the point (a, b) lies on the graph of f , then the point
(_____________) must lie on the graph of f ^-1 and vice versa. The
graph of f ^-1 is a reflection of the graph of f in the line

What you should learn
How to use graphs of
functions to determine
whether functions have
inverse functions

III. One -to-One Functions (Page 240)

To tell whether a function has an inverse function from its
graph , . . .

What you should learn
How to use the
Horizontal Line Test to
determine if functions are
one-to-one

A function f is one-to-one if . . .

A function f has an inverse function if and only if f is _____________

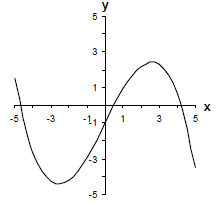
Example 2: Does the graph of the function at the right have
an inverse function? Explain.

IV. Finding Inverse Functions Algebraically (Pages 241-242)

To find the inverse of a function f algebraically , . . .

1)
2)
3)
4)
5)

What you should learn
How to find inverse
functions algebraically

Example 3: Find the inverse (if it exists) of f (x) = 4x - 5 .

Homework Assignment
Page(s)
Exercises