Linear Functions,Slope and Applications

•A function f is a linear function if it can be written as
f(x) = mx + b
where m and b are constants.
If m = 0, the function is the constant function f(x) = b. If m = 1 and b = 0, the
function is the identity function f(x) = x.

•Vertical and Horizontal Lines:
1. Horizontal lines are given by equations of the type y = b or f(x) = b. Are
horizontal lines functions ? What is the slope of a horizontal line?
2. Vertical lines are given by equations of the type x = a. Are vertical lines
functions? What is the slope of a vertical line?

• Linear Functions and Slope: Mathematically we define a line’s steepness or slope,
as the ratio of its vertical change (rise) to the corresponding horizontal change (run).
The slope m of a line containing the points (x₁, y₁) and (x₂, y₂) is given by:

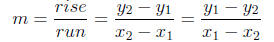
Example: Find the slope of the line containing the points (-3, 7) and (5,-1)

•Slope- Intercept Equation : The linear function f given by f(x) = mx + b has a
graph with slope m and y-intercept (0, b). May also be written as y = mx + b.
Example: Write the slope- intercept equation for a line with m = -2 and passing
through (-5, 1).

•The point-slope equation of the line with slope m passing through the point (x₁, y₁)
is
y - y₁ = m(x - x₁)

Example: Write the point-slope equation of the line that passes through (-3, 7) and
(-1,-5).

•Vertical lines are parallel. non-vertical lines are parallel if and only if they have the
same slope and different y -intercepts.
• Two lines with slopes m₁ and m₂ are perpendicular if and only if the product of
their slopes is -1.
m₁ * m₂ = -1

In other words, if m₁ is the opposite reciprocal of m₂ then the two lines are perpendicular.
Lines are also perpendicular if one is vertical (x = a) and the other horizontal
(y = b).
Example: Write an equation for a line passing through the point (-1, 6) and parallel
to the line 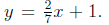Then write a second equation for the line perpendicular to
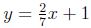and passing through (-1, 6).

Try these: pp93-94: 12, 28, 38, 48

Answers:
12.) slope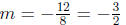
28.) slope m = 2/3 and y- intercept (0,-4)
38.)
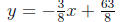
48.) neither