Rational Exponents
1. Recall: If n is a positive integer, then
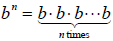 and, if
and, if 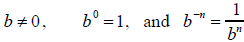 .
.
2. But, what if the exponent is a rational number and not an integer ? We want the rules for manipulating exponents to hold for the definition of a rational exponent.
3. For example, we want 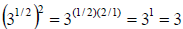 .
Thus,
.
Thus, 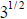 must be a number whose square is 3 and
a number whose square is 3 is
must be a number whose square is 3 and
a number whose square is 3 is 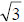 .
.
4. Definition of 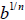 :
If
:
If 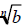 is a real number , (that is b ≥ 0 if n is
even), then
is a real number , (that is b ≥ 0 if n is
even), then 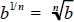 .
.
Note that the denominator of the exponent becomes the index of the radical.
5. Definition of
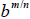 : If m and n are positive integers with m/n
in lowest terms, then
: If m and n are positive integers with m/n
in lowest terms, then
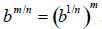
provided that 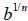 is a
real number . If
is a
real number . If 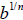 is not a real number then
is not a real number then
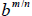 is not a real number .
is not a real number .
(This definition seems reasonable because we want
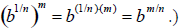
6. If all indicated roots are real numbers, then
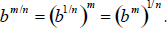
7. In radical form this means, provided that all roots are
real numbers, that

(The last form above is usually the easiest to use when evaluating a number with
a rational exponent .)
8. Definition of
 : If
: If 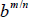 is a
real number and b ≠ 0, then
is a
real number and b ≠ 0, then 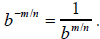
9. Be careful with minus signs . Recall that a negative exponent does not make the expression negative .
10. Rules for Rational Exponents: If r and s are rational numbers and a and b are real numbers for which the indicated expressions exist, then
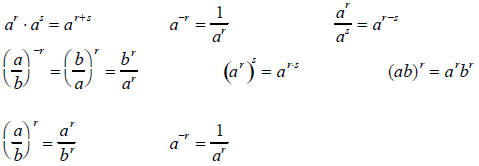
11. Many problems involving radicals can be simplified by converting the radical expression to one with rational exponents. Simplify the rational exponent and convert back to radicals.
12. Caution: 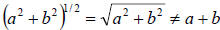 For example
For example
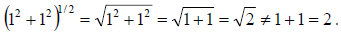
| Prev | Next |