Math 2090 Hour Exam 2 Solutions

No calculators permitted . You must show all your work to receive full credit. When carrying out row
operations on matrices , you may do more than one in each step , but you should always indicate what row
operation(s) you are doing.

1. (5 points) One of the vector space axioms is the unit property. What is the statement of this axiom?

Solution: For any vector .

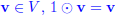2. (5 points) Which of the following matrices are in row-echelon form?

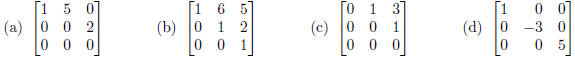
Solution: (b) and (c).

3. (5 points each) Suppose A is a 4 × 4 matrix with determinant 5.

(a) What is the rank of A?

Solution: 4

(b) What is detA²?

Solution: 25

(c) Does A necessarily have an inverse? (You should answer with one of “Yes,” “No,” or “It depends
on the matrix.” Give a brief justification for your answer.)

Solution: Yes. Any matrix with nonzero determinant is nonsingular.

4. (5 points) Consider the following system of equations :

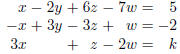
For what values of k does this system of equations have exactly one solution? Justify your answer.
(Hint: There is a trick to this question. It’s possible to answer it without doing any row operations on
the augmented matrix, although you can do row operations if you want to.)

Solution: None. The only way the system could have exactly one solution is if the rank of the coefficient
matrix was equal to the number of variables . There are 4 variables, but the coefficient matrix only has
3 rows, so it can’t possibly have rank 4.

5. (8 points) Consider the following system of equations:

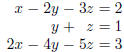
How many solutions does this system have? Give a brief justification, but do not solve the system .
(Hint: You will save yourself a lot of work if you look at Problem 7 first.)

Solution: One. The coefficient matrix is nonsingular, and any system with a nonsingular coefficient
matrix has a unique solution.

6. (15 points) Find the following determinant.

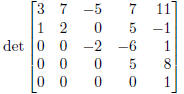
Solution:

This last matrix is in upper-triangular form, so its determinant is the product of the diagonal entries:
1 · 1 · (−2) · 5 · 1 = −10. To get this matrix, we did A_1,2(−3) (which didn’t change the determinant)
and P_1,2 (which changed its sign). So the determinant of the original matrix is 10.

7. (15 points) 2 Find the inverse of the following matrix.

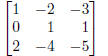
Solution:

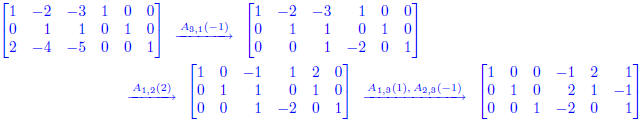
The inverse matrix is .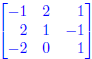

8. (16 points) In each of the following questions, V is a vector space, and S is a subset of V . Determine
whether S is a subset of V , and justify your answer. You should only answer two of the three
parts.

(a) V = R², and S is the set of points on the x- and y-axes.

Solution: No. S is not closed under addition. For example, (1, 0) is a point on the x-axis, and
(0, 1) is a point on the y-axis, but their sum (1, 1) is not on either axis.

(b) V = M₂(R), and S is the set of matrices with all 0’s on the second row.

Solution: Yes. If you add two such matrices, the answer will also have all 0’s on the second row,
and if you multiply such a matrix by a scalar, you’ll still have all 0’s on the second row.

(c) V = C²(R), and S is the set of functions satisfying the equation y'' = 5y + 2.

Solution: No. The equation y'' − 5y = 2 is nonhomogeneous, and the set of solutions to a
nonhomogeneous equation is not a subspace.

9. (16 points) Consider the set V = M₂(R). Instead of the usual matrix operations, let us define vector
addition ( ) and scalar multiplication for this set as follows:

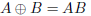(matrix multiplication)
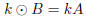(ordinary scalar multiplication for matrices)

Answer two of the following three parts:

(a) Give a reason why V with these operations is not a vector space. (That is, name an axiom that
isn’t true for V . You can just refer to the axiom by name; you need not state it.)

Solution: Here are several possible reasons:

i. The operation 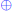is not commutative.
ii. Not all elements of V have additive inverses. (See part (c).)
iii. The distributive property for scalar multiplication over vector addition doesn’t hold: that is,
it’s not true that



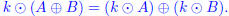
(The left side of the equation is equal to kAB, where as the right side is (kA)(kB) = k²AB.
Since kAB ≠ k²AB, the distributive property is false.)

(b) Although V is not a vector space, there is an element of V that satisfies the “Existence of a zero
vector” axiom. What is the zero vector in V ? No justification is required.
Solution: The zero vector is the identity matrix .

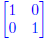(c) Do the following matrices have additive inverses? Give a brief justification for your answers. (For
cases where the additive inverse exists, you are not required to find the additive inverse, although
you can if you want to— calculating it is a way of proving that it exists!)

Since is matrix multiplication and the zero vector is the identity matrix, the notion of “additive
inverse” for is the same as what we normally just call “the inverse” of a matrix. Therefore, this
question is asking whether the following matrices have inverses.



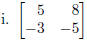
Solution: Yes. The determinant of this matrix is 5(−5)−(−3)8 = −1 ≠ 0, so the matrix has
an inverse.



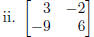
Solution: No. The determinant of this matrix is 3·6−(−9)(−2) = 0, so the matrix is singular.