Math 222 Final Exam

Instructions: Write answers to problems on separate paper. You may NOT use calculators or any
electronic devices or notes of any kind. Loads of points are possible on the exam, but the highest
grade that I will award is 115 points.

1. (5 points) Consider the area under the curve y = 1/x³, where x ≥ 1. A vertical line x = b
splits this region into two equal areas. Find the value of b .

2. (4 points) Find the average value of the function y = cosx over the interval [-π/2,π/2].
(Evaluate completely to get an exact numerical answer .)

3. (4 points each) Evaluate each of the following integrals.

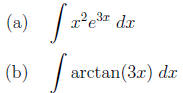
4. (4 points each) Evaluate each of the following integrals.

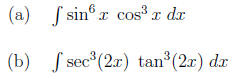
5. (4 points each) Evaluate the integrals.

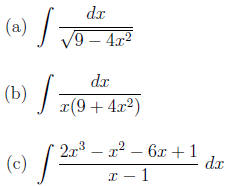
6. (4 points each) Evaluate each definite integral completely and simplify . If the integral diverges,
say so and state how it diverges (e.g., to ∞ or -∞). (Very little credit will be given for answers
with no work or incorrect reasoning.)

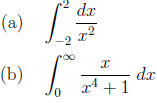
7. (3 points each) The portion of the curve y = tan 2x, -π/6 ≤x ≤ π/6 is rotated about each
of the following axes. Calculate the areas of each surface of revolution formed. (Set up the
integrals.)

(a) the y-axis
(b) the x-axis
(c) the line x = π/2

8. (8 points) Find the centroid 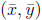 of the region R bounded by y = x(x - 1) and y = 2. Don't
merely set this one up - calculate it completely and simplify. And you need to get this region
right, as the next few problems use it, too.

9. (4 points) Let R be the region described in the previous problem . Find the volume of the solid
of revolution formed by rotating R about the line x =-1. Set up the integral completely but
don't evaluate it.

10. (4 points) Let R be the region used in the previous problems. Find the volume of the solid of
revolution formed by rotating R about the line y = -1. Again just set up the integral.

11. (6 points) Let R be the region used in the previous problems. Consider the intersections of
vertical lines in the xy-plane (lines parallel to the y-axis) with the region. (The region is is
the union of such segments.) Treating each of these line segments as a base, erect squares
perpendicular to the xy-plane on each segment. Find the volume of the solid formed by the
union of those squares. Just set up the integral (although it isn't very difficult to evaluate and
simplify it ).

12. (4 points) State the definition of a convergent sequence. (Hint: It has an epsilon in it.)

13. (3 points) State (the hypotheses and conclusions of) the monotone convergence theorem.

14. (2 points each) Determine whether each of the following sequences {a_n } converges or diverges
for the given an. If it converges, find its limit. If it diverges to +∞, say so. If it diverges to
−∞, say so. If it diverges in some other way, say how. No credit for "diverges" or "converges",
but no extra penalties for incorrect answers.

15. (3 points) State the precise hypotheses and conclusion of the theorem we call "the Integral
Test".

16. (3 points) State the precise hypotheses and conclusion of the theorem we call " the Root "Test".

17. (2 points for each correct answer, ¡1 for each incorrect answer, no penalty for blanks) Deter-
mine whether each of the following series is absolutely convergent, conditionally convergent
or divergent. (Also, see extra-credit problem (??) for a related question.)

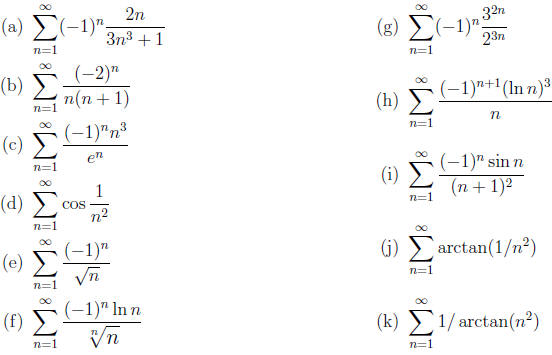
18. (3 points each) Find the intervals of convergence of each of the power series . (I.e., state all real
values of x for which the series converges.)

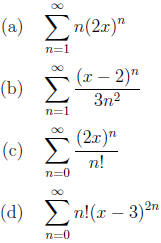
19. (3 points each) Write down (you needn't derive it if you can just write it) the Maclaurin series
expansion (Taylor series centered at c = 0) for each of the functions below. You may write four
nonzero terms for each or for one extra point each, write the series in closed ( summation ) form.

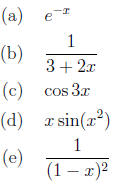
20. (3 points) Give the first four nonzero terms of the Taylor series for the following. Again, you
needn't derive it if you can just write it.

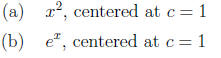
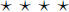Extras
(5 points per )

A.) () Use a theorem of Pappus to evaluate the volume of the solid obtained by rotating the figure
ABC about the line x = 1, where ABC is the triangle with vertices A = (2, 3); B = (2, 5); C =
(5, 5):

B.)() Integrate: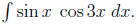

C.) () Write four terms of the binomial expansion for 4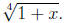

D.) () Write the repeating decimal :0246666666666 ... as a ratio of integers.

E.) () Write the first three nonzero terms for the Maclaurin series of cos x and sin x. Give the first
three nonzero terms of the power series for sin x cos x by directly sufficiently many terms of the
two series. Then get he result a cooler way, if you can. Also, use long division of series to get
the first three nonzero terms sec x by dividing the series for cos x into the constant 1. I suppose
you could check your answer by using Taylor's formula for the Maclaurin series of sec x (but I
wouldn't want to).

F.) () Maybe you can evaluate the following limit.

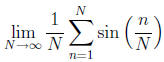
G.) ( Don't try this at home. No - DO try it at home, but don't try it here. Show that the area
under the curve y = tan x from 0 to π/2 is infinite. Then show that the area under the curve
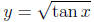from 0 to π/2 is equal to 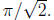It aint that easy. Send me email for hints. I'll post
this final exam online. (Remind me if I forget).

H.) (... ) Ask a question you wish I had asked and answer it. Points may vary. Offer void where
prohibited by time!