Fractions and Decimals and Percents
Sec 2.6 and 2.7

Rational Numbers - A number that can be written as a fraction, where the
numerator and denominator are integers, and the denominator cannot equal
zero.

Fractional Review – Reducing fractions

Decimals:
$4325.72
Notice that the decimal point is placed between the ones column and the tenths
column to show where the whole-number portion ends and where the decimal (or
fractional) portion begins. Decimals are read as if they were written as fractions
and the decimal point is read “and.” In fact, the word “and” should only be used
to indicate where the decimal point is located.

Writing a check:
Four thousand three hundred twenty-five and 72/100

Fraction to Decimal:
We can change any rational number in fraction form into decimal form by
dividing .

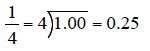
Terminating decimals : A decimal that has a finite number of nonzero digits to
the right of the decimal point. Examples: 0.25, 0.5, 0.175

Fractions with Terminating Decimal Representations
 

Let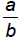 be a fraction in simplest form. Then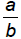 has a terminating decimal
representation if and only if b contains only 2s and/or 5s in its prime factorization.
Remember that a percent is a fraction with a denominator of 100.
The word percent is abbreviated from the Latin word per centum meaning per
hundred, on hundred or hundredth.

The symbol to denote percent is %. Thus, 25 percent is written as 25%.
Remember that percent can be expressed in the form of a fraction (or a decimal)
and vice-versa. Thus we have:

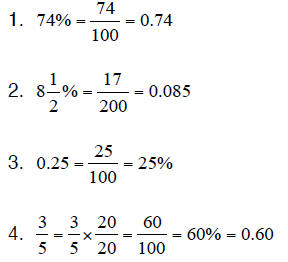
Ordering Decimals
Terminating decimals can be compared using a number line, by comparing them
in their fraction form, or by comparing place values one at a time from left to right
just as we compare whole numbers.

Repeating decimals: A decimal that has a digit or group of digits that repeat
over and over. Example: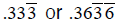

Fractions with Repeating, Nonterminating Decimal Representations

Let 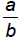be a fraction written in simplest form. Then 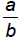has a repeating decimal
representation that does not terminate if and only if b has a prime factor other
than 2 or 5.

How to write terminating decimals as fractions

Example:

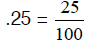
How to write repeating decimals as fractions

Example of writing a repeating decimal as a fraction when there are only
repeating digits:

Let n =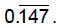

Thus 1000n =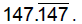

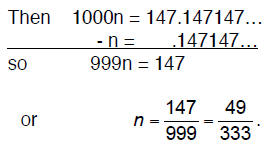
Example of writing a repeating decimal as a fraction when there are nonrepeating
digits as well as repeating digits:

Example:

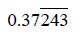
Let n =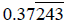

Multiply “n” by the appropriate number so the decimal point moves behind the
first group of repeating numbers. Here that would be 100000. So you would
have:

100000n = 37243.243

Now multiply by the appropriate number so the decimal point moves behind the
non-repeating digit(s) and in front of the repeating digit(s). So you would have
the following:

100n = 37.243

Now subtract the second from the first:

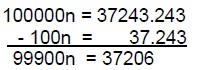
Notice how this subtracts off the repeating part.

Now solve for n:

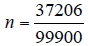
Next simplify the fraction to its lowest terms :

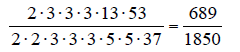
Finally, check on your calculator or with long division to be sure your answer is
correct!

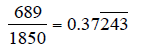
If you do enough of these you will realize there is a quicker way:

Let’s look at the same example:

Example: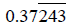

Now subtract off the non-repeating part (37) from the non-repeating and
repeating part (37243).

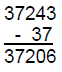
You can see that when you did this in the traditional manner, in the first example
that after you moved the decimals over the correct number of times and then
subtracted you were essentially subtracting the non-repeating part from the nonrepeating
and repeating part as we did in this example.

Now that we have found the numerator, we need to find the denominator.

To find the denominator we want to remember the pattern we did previously for a
number where zeros come before the repeating part such as: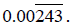

We got this number 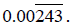by replacing the non-repeating part of the original
problem 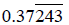with zeros.

Remember if the number is one such as 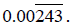, the denominator would be
99900 since there are three repeating numbers which give us the 999, and two
zeros between the decimal and repeating numbers, which gives the 00.

So, once again we have: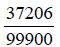

From there we still need to reduce as we did at the top of this page.

Generalization about Decimals for Rational Numbers
Every rational number can be expressed as a terminating or repeating decimal.

Irrational Numbers are numbers that can be written as decimals, but not as
fractions.

Examples of irrational numbers:

The Square root of 2:

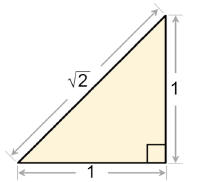
Other examples of Irrational Numbers:

	Pi is a famous irrational number. People have calculated Pi to over one million decimal places and still there is no pattern. The first few digits look like this: 3.1415926535897932384626433832795 (and more ...)
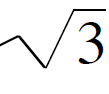	Many square roots, cube roots, etc are also irrational numbers. √3 : 1.7320508075688772935274463415059 (etc)
	The number e (Euler's Number) is another famous irrational number. People have also calculated e to lots of decimal places without any pattern showing. The first few digits look like this: 2.7182818284590452353602874713527 (and more ...)
	The Golden Ratio is an irrational number. The first few digits look like this: 1.61803398874989484820... (and more ...)