The Quadratic Formula and Discriminant

The solutions of the quadratic equation 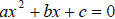are given by the

Quadratic Formula :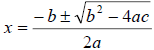

Note: The quadratic formula is obtained by completing the square and solving for x. Try it! ☺

Example:

For the quadratic equation 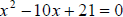, we have a = 1, b = -10, and c = 21, so

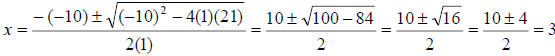and 7
 

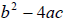is called the discriminant because it discriminates among kinds of solutions.

If a, b, and c are integers, then

If Discriminant	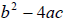Then ( Kind of Solutions )
= 0	One rational solution
> 0 and the square of an integer	Two rational solutions
> 0 and not the square of an integer	Two irrational solutions
< 0	Two complex (imaginary) solutions

Examples:

1. 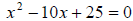has exactly one rational solution because the discriminant = 0

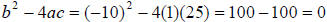(Show that x = 5 is the solution .)

2. 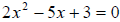has exactly two rational solutions because the discriminant > 0
and the square of an integer .

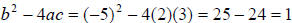( Show that 1 and 3/2 are the solutions .)

3. 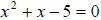has exactly two irrational solutions because the discriminant > 0 and
the square of an integer.
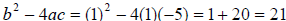(Show that 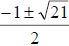are the solutions.)

4. 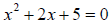has exactly two complex solutions because the discriminant < 0.

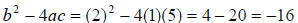(Show that 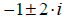are the solutions.)