Putnam Problem Solutions

A story in the June issue of E&S about
the Putnam Mathematical Competition
and Caltech's star competitor Peter Shor
(BS '81) left some problems for readers to
tackle. Here are Shor's answers.

Problem B-3, 1980
For which real numbers a does the
sequence defined by the initial condition
u₀ = a and the recursion u_n+1 = 2u_n
- n²  have u_n > 0 for all n ≥ 0?

Express the answer in the simplest
form.)

You can make the recursion easier by
defining v_n's by

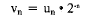
U_n will be positive whenever v_n is positive.

Then 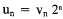, and v₀ = u₀ = a.
The formula u _n+1 = 2u_n - n²
becomes
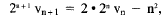
or
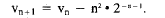
This gives

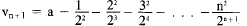
v_n will be positive for all n if

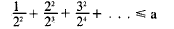
Now, if x = 1/2 this is
x² + 2²x³ + 3²x⁴ + . . .

To sum this series , consider

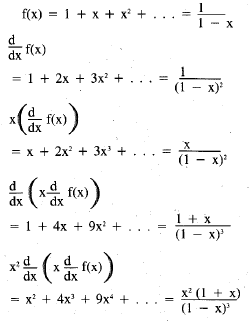
and this series is what we want with x = 1/2.
So, the series converges to 3, and the
answer is a ≥ 3.

Problem B-4, 1980
Let A₁, A₂, ... , A₁₀₆₆ be subsets of a
finite set X such that |A₁| > 1/2|X| for 1 ≤ i
≤1066. Prove there exist ten elements x₁ ,
. . . , x₁₀ of X such that every A_i contains
at least one of x ₁, . . . , x₁₀.

(Here |S| means the number of elements
in the set S.)

We can find an element x₁ that is contained
in more than half the sets A_i. If
there were no such x₁, then |A₁| + |A₂| +
... + |A₁₀₆₆| would be less than or equal
to 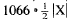because each x is in at
most half the A_i's. But for each A_i, |A_i| >
1/2|X|·

Consider only the sets A_i with x₁ not
contained in A_i. There are at most 532 of
these, and each of them contains more
than half of the elements of X. Repeating
the argument above, there is an x₂ contained
in more than half of these 532
remaining sets, leaving at most 265 sets
without x₁ or x₂. Repeating this ten times,
you get x₁, x₂, ... , x₁₀, with each A_i
containing one of them.

Problem A-6, 1978
Let n distinct points in the plane be
given. Prove that fewer than 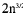pairs of
them are unit distance apart.

Draw a circle of radius 1 around each
of the points P_i. Define e_i as the number
of points p on the circle around P_i.
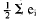is the number of pairs of points
at distance j, since each pair gives two
points on the circles. We can assume e_i ≥ 1
for all i, since otherwise we have a point
unit distance from no points.

Each pair of circles has at most two
intersections, so there are at most n(n-1)
intersections. The point P_i occurs as an
intersection 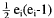times, so we have

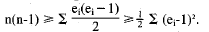
By the Cauchy-Schwarz inequality,

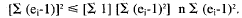
So, combining the above equations ,

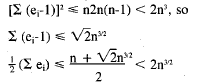
And finally, there's Problem A-4 from
1980, the first part of which was solved in
the June issue, leaving (b), the harder
part, for readers.

(a) Prove that there exist integers a, b, c,
not all zero and each of absolute value
less than one million, such that

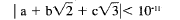
(b) Let a, b, c be integers, not all zero and
each of absolute value less than one million.
Prove that

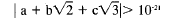
In (b) you can multiply by conjugates to
get rid of the square roots :

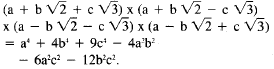
If a, b, and care all integers, then this
will be an integer, and if it's not equal to
0, it has to be of magnitude at least 1.

In the first part of the problem we
showed that a number of this form had to
be less than 10⁷, so if the product of the
conjugates is not 0, then we have a +
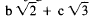times three factors that
are less than 10⁷ yielding something bigger
than or equal to 1, and therefore

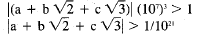
and we're done.

Now all we have to do is show that the
product of the conjugates cannot be equal
to 0, and we can do this by proving that
it's impossible for any of the four conjugate
factors to be 0. If
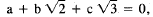, say,

then

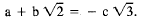
Now, squaring both sides, we get

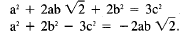
If a and b are not 0, then this last equation
could be used to express 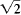as a quotient
of integers, which is impossible since
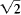
isn't a rational number . So it only remains
to consider the possibility that a = 0 or b
= 0. If b = 0, then

which would make 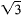  a ratIonal number
unless c = 0. But if c is 0, then obviously
a is 0, so a, b, and c are all 0, contrary to
assumption. So the only remaining possibilities
are in the case a = 0, b ≠ 0.
In this case

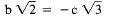
so we get

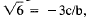
which is impossible because 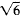is not
rational, and this completes the argument.
39