Notes for Rational Functions

Topics: Graphing Rational Functions , Finding Vertical and
Horizontal Asymptotes, Applications of Rational Functions

This video lesson has lots of material that you will omit. You may want to go through this handout
first, the book second, then look at the video if necessary.
Recall: A rational number can be expressed as the quotient of two integers .
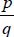A rational function is the quotient of two polynomials 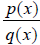, where q(x) does not equal 0.

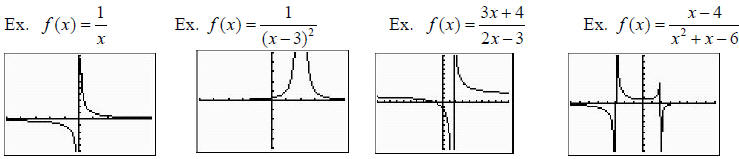
*Remember when entering fractions like the 2^nd, 3^rd and 4^th examples into Y₁, you must use ( )
around each numerator and/or denominator since they have a sum or difference in each part. I have
set the WINDOWS at either [-8, 8, 1] x [-8, 8, 1] or [-5, 5 1] x [-5, 5, 1]
* The graphs above are in from a MODE that is CONNECTED, where the calculator is doing its
best to draw you a continuous graph. The MODE that is DOT will give you a graph like:

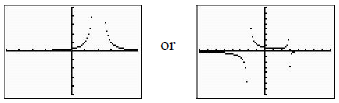Choose whichever you prefer , as long as you realize the difference in the looks of the two . More about why they are different later …

I. Graphing Rational Functions (p. 350 – 353)
These graphs are not your every-day graphs. They have curves and bends that are not parabolic,
cubic, or any like we’ve seen.
They have some common characteristics that will help to sketch them:
1. The domain is all values except the ones that make the denominator become 0.
Ex. 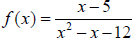has a denominator that factors to (x – 4)(x + 3) and that makes the domain
become (−∞,−3)∪(−3, 4)∪(4,∞)which excludes –3 and 4.
2. For reasons on the video and in the text at the bottom of page 350, there are “bumper lines” that
the graphs get very close to, but don’t cross over, and they are called asymptotes.
A. The Vertical Asymptote is a line x = a (number), where the graph approaches infinity (goes out
the roof) on one side and approaches negative infinity (goes to the cellar) on the other side, as the
values get closer and closer to the number. The values that were excluded in the domain become the
Vertical Asymptotes. The Vertical Asymptote(s) are found by factoring the denominator of the
function. Those values that we would exclude from the domain since they would cause the
denominator to be = 0 become the values that are the Vertical Asymptote equations . There may be
more than one, depending on the factoring.
Ex. The Vertical Asymptotes of the example in #1 are x = – 3 and x = 4. The calculator is trying
to draw the Vertical Asymptotes in CONNECTED mode below.

Note that the “jags” in the graph happen at –3 and 4.

B. The Horizontal Asymptote is the horizontal line y = b ( number) that the graph “bumps”.

Here are the three cases for finding a Horizontal Asymptote, if the rational function has one. They
all depend on comparing the degrees of p(x) and q(x):

1. If the degree of the numerator polynomial is less than the degree of the denominator polynomial,
then the x-axis or y = 0 is the horizontal axis. (Similar to a proper fraction where the numerator is
less than the denominator)

Ex. 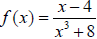The degree of each is: 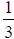, which is a “proper-degreed” situation, so H.A. is y = 0.

2. If the degree of the numerator polynomial is the same as the degree of the denominator
polynomial, then the line 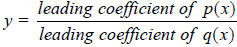is the Horizontal Asymptote.

Ex. 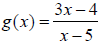. The degree of each 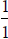is, which is a tie. So the H. A. is .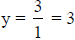

3. If the degree of the numerator polynomial is greater than the degree of the denominator
polynomial, then there is no horizontal asymptote. (Division by 0 in the video)

*We do not include anything that has to do with Oblique Asymptotes.
* The graph of a function never crosses a vertical asymptote.
* The graph of a function may sometimes cross a horizontal asymptote.
*Asymptotes are not part of the graph of the rational function, but are necessary to give information
about the graph.

Graphing a Rational Function (p. 356 blue box): Here’s what you do-
1. Enter the function into the calculator, being careful to include ( ) around any numerator or
denominator that needs it. This will give you a general idea of the turns that the sketch will take.
2. Find the Vertical Asymptote(s) by finding the zeros of the denominator —factor if possible, or use
quadratic formula (not on the test). Draw them on the graph as dotted lines going up and down.
3. Find the Horizontal Asymptote, if there is one and sketch it as a dotted line going left-right.
4. Find the y-intercept by evaluating the function at x = 0 (Substitute) or look in TABLE.
5. Find the x-intercept(s) by finding the zeros of the numerator by solving p(x) = 0 by factoring or
quadratic formula
6. Find other points from the TABLE to give it the general shape that you see in the calculator
viewscreen.

If the function has a common factor between the numerator and the denominator, then there will be a
“hole” at that value of the graph.

Ex. 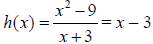when reduced.

Don’t be fooled by what you see in the calculator on this one! The domain of this function must still
exclude the –3 value that cannot happen. The domain is (−∞,−3)∪(−3,∞) . Please make the “hole”
in your sketch a clearly open circle at the spot on the line in the first quadrant where it would be.
*Note that reduced fraction doesn’t give a Vertical Asymptote and the “improper degreed”
polynomials that make the function mean that there is no Horizontal Asymtote, either.

II. Applications of Rational Functions
Ex. A drug is injected into a patient and the concentration of the drug in the bloodstream is
monitored. The drug’s concentration, C(t), in milligrams per liter, after t hours is modeled by

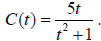
a. Sketch the graph using the graphing calculator. Do you need to see all of the 4 quadrants to work
this problem?
b. Name the Vertical Asymptote, the Horizontal Asymptote, the y-intercept and the x-intercept.
Note that there may be an answer to these, or there may not be an answer.
c. What is the drug’s concentration after 3 hours?
d. Will the drug ever leave the patient’s bloodstream? (Hint: use what you know about the
horizontal axis)
e. When did the patient receive the maximum amount of this drug?

(Answers on the next page.)

Answers to the Application Example:

a.

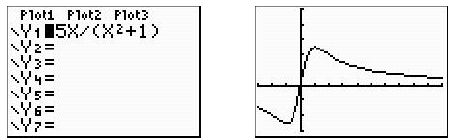	Graph is [-3, 10, 1] x [-3, 5, 1]

b. Vertical Asymptote: none, since x² + 1 cannot be factored.
Horizontal Asymptote: y = 0, since the fraction is a “proper degreed” one, where the num < den
y-intercept: (0, 0)
x-intercept: (0, 0) only
c. The concentration after 3 hours can be found in the TABLE or by substitution .

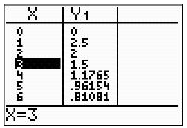The patient had approximately 1.5 milligrams per liter of fluid in his or her bloodstream after 3 hours.

d. The drug will never leave the patient’s bloodstream, since there are no other x intercepts other
than the origin.
e. Use 2^nd CALC 4:Maximum.

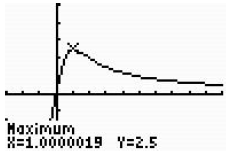The maximum dosage that the patient received was after 1 hour, when he/she received 2.5 milligrams of medication.